2018年度　江戸川取手中学過去問【算数】大問３解説

問題ＰＤＦ
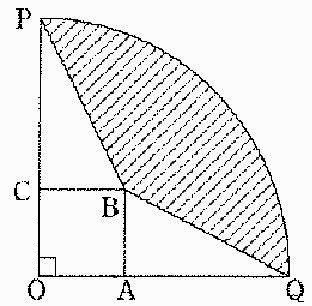
下の図のように、半径12ｃｍ、中心角90°のおうぎ形ＯＰＱの内部に、
一辺が４ｃｍの正方形ＯＡＢＣがあります。このとき、次の問いに答えなさい。

（１）
図中の斜線部分の面積を求めなさい。

（２）
ＯＰ上に点Ｍをとり、ＭＰ、ＭＱと曲線ＰＱで囲まれた図形の面積が（１）で求めた面積と等しくなるときのＰＭの長さを求めなさい。

＠解説＠
（１）

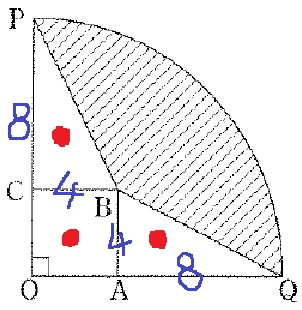
全体から３ヶ所をひく。
12×12×3.14÷４－４×４－４×８÷２×２
＝113.04－48＝65.04ｃｍ²

（２）

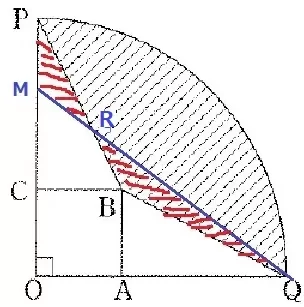
ＭＱとＰＢの交点をＲとする。
Ｐ・Ｂ・Ｑに囲まれたところと、Ｐ・Ｍ・Ｑに囲まれたところが等しいということは、
Ｐ・Ｒ・Ｑに囲まれたところを除いた△ＰＭＲと△ＱＢＲが等しい。

△ＰＭＲと△ＱＢＲに四角形ＭＣＢＲを足すと、
△ＰＣＢと四角形ＭＣＢＱの面積も等しい。
△ＰＣＢは16ｃｍ²なので、四角形ＭＣＢＱも16ｃｍ²
△ＭＯＱ＝正方形ＯＡＢＣ＋△ＡＱＢ＋四角形ＭＣＢＱ
＝16×３＝48ｃｍ²
ＯＭ＝48×２÷12＝８ｃｍ
ＰＭ＝12－８＝４ｃｍ

＠別解＠

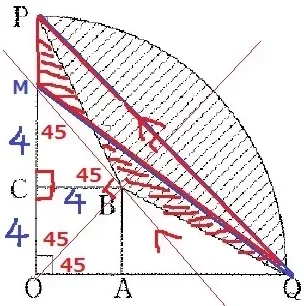
Ｂを通る、ＰＱに平行な線をひく。
等積変形から、△ＢＰＱ＝△ＭＰＱ
△ＯＰＱは直角二等辺で、ＯＢは∠ＰＯＱの二等分線（正方形の対角線だから）。
ここから、ＯＢとＰＱとの平行線は直角に交わる。
△ＯＢＭも直角二等辺、△ＢＣＭも直角二等辺。
ＭＣ＝ＢＣ＝４ｃｍなので、ＰＭ＝４ｃｍとなる。