問題ＰＤＦ
図１のような、１辺の長さが１ｃｍの正方形の紙①があり、左下の頂点をＯとします。正方形の紙①の対角線の長さを１辺とする正方形の紙②を、図２のように正方形の紙①に重ねて置きます。
（１）
正方形の紙②の面積を求めなさい。
正方形の紙②の対角線の長さを１辺とする正方形の紙③を、同じように正方形の紙②に重ねて置きます。このようにして、正方形の紙④、⑤、･･･を重ねて置いていきます。
（２）
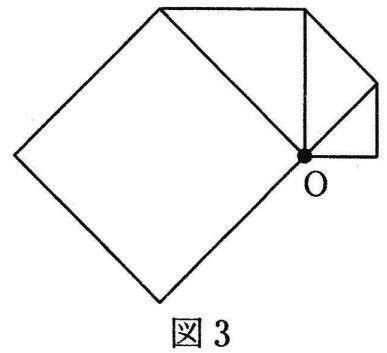
図３は、正方形の紙④までを重ねて置いた図です。
このとき、２枚の紙が重なっている部分の面積を求めなさい。
（３）
正方形の紙⑤までを重ねて置いたとき、紙が置かれている部分のうち、
紙が重なっていない部分の面積を求めなさい。
（４）
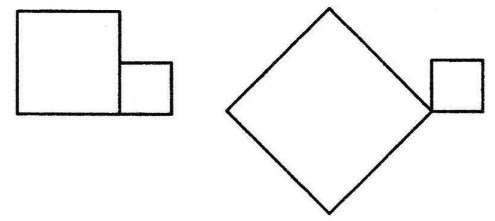
正方形の紙⑪までを重ねて置いたとき、最も多くの枚数の紙が重なっている部分の面積を求めなさい。ただし、下の２つの図のように、正方形の紙の縁どうしが重なっているだけの場合は、紙が重なっているとは考えません。
＠解説＠
（１）
●２つが１ｃｍ2なので、●４つは２ｃｍ2。
（２）
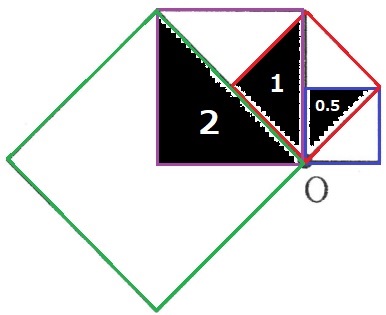
実際に描いてみると、２枚重なっている部分は２倍ずつ増えている。
0.5＋１＋２＝3.5ｃｍ2
（３）
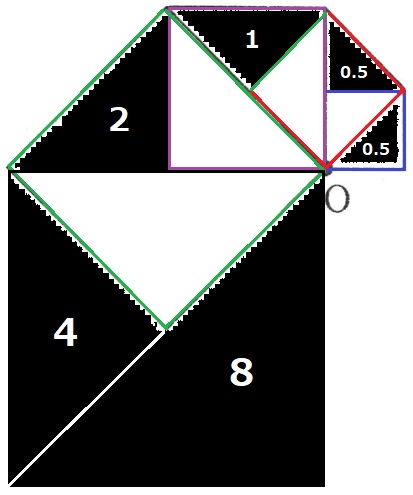
最初に0.5が２ヶ所ある。
最後は４ではなく、８が追加される点に注意！
0.5＋0.5＋１＋２＋４＋８＝16ｃｍ2
（４）
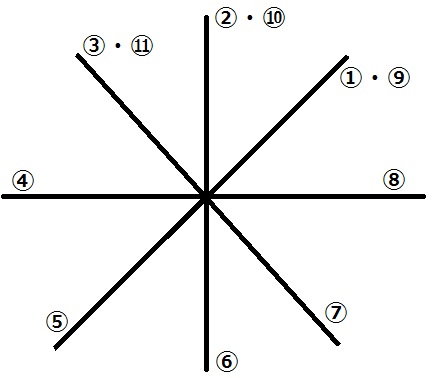
正方形の対角線に注目してみる。
45度ずつ反時計回りに重ねていく。
⑧の対角線が右側に伸び、⑪は③と重なる。
そして、対角線の両サイドの部分に新しい正方形が足されていく。
（２）で１周目に２枚重なっている部分に目をつける。
⑪の右側までで４枚重なる部分はうえの通り。
よって、1.5ｃｍ2。
＠余談＠
⑬までやると、こうなります。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント