問題PDF
(1)③
赤玉と白玉が7:13の割合で袋の中に入っています。
この袋の中に赤玉3個、白玉2個を加えたところ、赤玉と白玉は9:16の割合になりました。
最初の袋の中に入っていた赤玉は何個ですか。
④
2/11=0.181818…のように、2/11は1と8の数字がくりかえされる小数で表すことができます。
8と1の数字がくりかえされる0.818181…を分数で表しなさい。
⑥
重さが異なる4つのおもりA、B、C、Dがあります。
この4つのおもりからいくつか選んでてんびんにのせたところ、
次の図のような関係になりました。
4つのおもりA、B、C、Dを、左から軽い順に答えなさい。

⑦
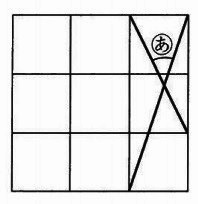
下の図は、同じ正方形を9個並べて、1つの大きな正方形をつくったものです。
図のように2つの直線が交わっているとき、(あ)の角度は何度ですか。
(2)
ゆりさんはA、B、Cの3つの水そうで熱帯魚を飼っています。
3つの水そうの体積と水そうの中にいる熱帯魚の割合は図1、図2のようになっていて、
Aの水そうの体積は0.06m3で、1m3当たり250匹の熱帯魚が入っています。
ゆりさんは熱帯魚を5匹増やすことにし、3つの水そうに入る1m3当たりの熱帯魚の数が
同じになるように入れ直したいと考えました。
入れ直した後、Cの水そうには何匹の熱帯魚が入っていますか。

(3)
下の図のように立方体を規則的に重ね、底の面も含めてすべての表面をペンキで塗ります。
7段まで積み上げたとき、1面だけが塗られた立方体の個数を求めなさい。

(4)
30cm離れた2地点A、Bがあります。
点P、Qが1回目に出会った後、点PはBに、点QはAに着いてから折り返し、
点P、Qは2回目に出会い止りました。
下のグラフは出発してからの時間とPQ間の距離を表したものです。
後の各問いに答えなさい。
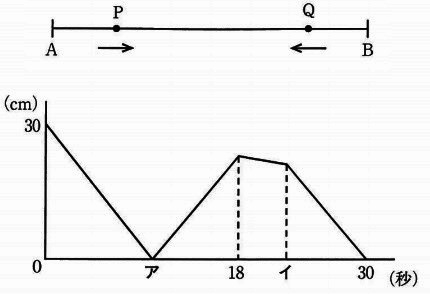
①アの値を求めなさい。
②イの値を求めなさい。
(6)
下の図は、中身の見える立方体の容器の中に入れた棒を、正面と真上から見たものです。

(7)
下の図は、平行四辺形の紙から大きさの異なる平行四辺形の紙を切り取ったものです。
この紙を1本の直線で二等分するためには、どのように切ればよいですか。
切り目を解答用紙にかきなさい。なお、切り目をかく際に用いた線は消さないでおくこと。 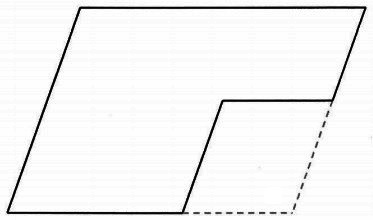
(8)
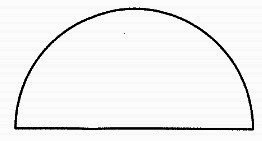
下の図1のように、円形の折り紙を、直径を折り目にして半分に折ります。
半分に折ったあと、図2のように直線で切り目を入れて開き、いくつかに分かれているかを調べます。
例えば、図2のような1本の直線で切り目を入れて開くと、もとの円形の折り紙は3つの部分に分かれます。
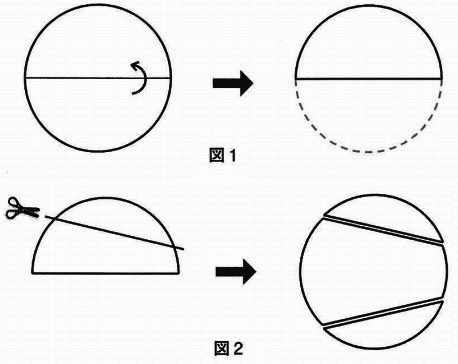
3本の直線で切り目を入れて開いたところ、もとの円形の折り紙は8つの部分に分かれました。
どのように切り目を入れましたか。切り目を解答用紙にかきなさい。
(10)
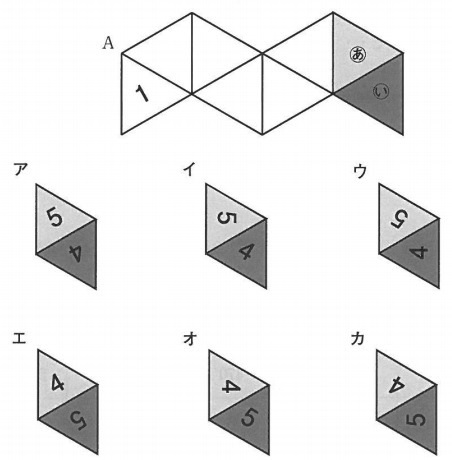
下の図1のように、1から8までの数字が書かれた8つの正三角形でつくられた立体があります。
図1で頂点A、Bを上下にして、①の方向から頂点Cを正面に見たものが図2、
②の方向から頂点Dを正面に見たものが図3です。

この立体で次の展開図を考えるとき、面(あ)と面(い)として正しいものを選びなさい。
(11)
ある食堂では、350円のA定食、400円のB定食、450円のC定食があり、そのうちからどれか1つを選んで注文します。また、追加として、50円でごはん大盛りを、120円でサラダを選ぶことができます。ある時間帯に、この食堂を利用した人数と支払金額を調べたところ、A定食を注文した人の支払金額の平均は417円であり、B定食を注文して支払金額が400円だった人は6人でした。このとき後の各問いに答えなさい。

①この食堂での注文の仕方は、全部で何通りありますか。
②今回の調査の結果は下の表のようになりました。A定食を注文した人数を求めなさい。

@解説@
(1)③
関係性を図示する。

合計に注目。
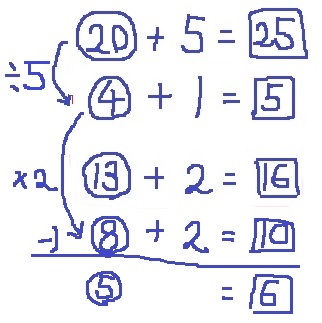
合計を÷5すると、④+1=□5
×2して、⑧+2=□10
この式を、⑬+2=□16からひくと、⑤=□6となる。
⑳を□で表す→⑳×□6/⑤=□24
□25-□24=□1が5個に相当する。
□9=5×9=45個
最初の赤玉は、45-3=42個
④

□=0.818181…とおく。
小数点以下をそろえるために100倍する→100×□=81.818181…
両辺を引くと、99×□=81
□=81÷99=9/11
@別解@
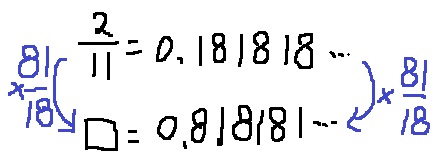
0.1818…の無限小数(2/11)を×81/18倍すれば、0.8181…の無限小数になるので、
2/11×81/18=9/11
⑥

釣り合っている2つの天秤に注目する。
A+A=B+D
÷2すると、A=(B+D)/2
つまり、AはBとDの平均になる。
同様に、B=(C+D)/2から、BはCとDの平均。
数直線で表す。
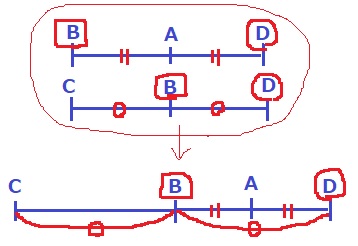
BとDを手掛かりに、1本の直線で示すと上のようになる。
A+B>C+Dから、A・B側が大きくなくてはならない。
すなわち、上の数直線では右側の値が大きい。
軽い順になおすと、C<B<A<D。
⑦
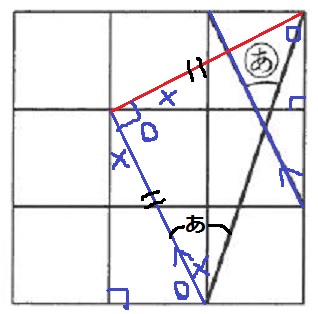
青い線を平行移動。
この線は2×1の長方形の対角線で、赤い線も同様。
○+×=90°で印をつけて角度を調べると、直角二等辺三角形があらわれる。
(あ)を同位角で移動させて、(あ)=45°
(2)
Aの水槽にいる熱帯魚は、250匹×0.06m3/1m3=15匹
すべての熱帯魚は、15匹×100%/20%=75匹
5匹加えて、80匹となる。
『3つの水そうに入る1m3当たりの熱帯魚の数が同じになる』
→水槽の体積比に案分する。
A:B:C=3:5:2より、Cの水槽は80×2/10=16匹
(3)
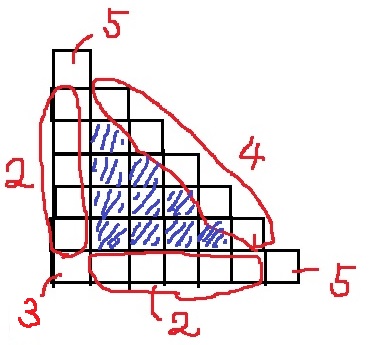
1面しか塗られないのは10個。
これが3面あるので30個。
(4)①
PとQのどちらが速いか不明だが、どちらが速くても設問に影響しないので、
以下、PがQより速いことを前提として図示する。
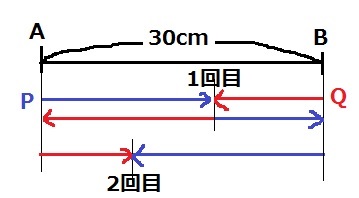
2回目の出会いまで、PとQは2人でA-B間の距離の3倍を動く。
1回目の出会いはA-B間の距離だから、30秒÷3=10秒
②
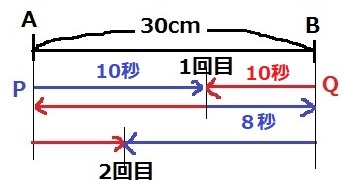
Qが10秒で動いた距離を、Pは18-10=8秒で動く。
PとQの時間の比は、P:Q=8:10=4:5
QがAに到着するのは、18秒×5/4=45/2秒
(6)
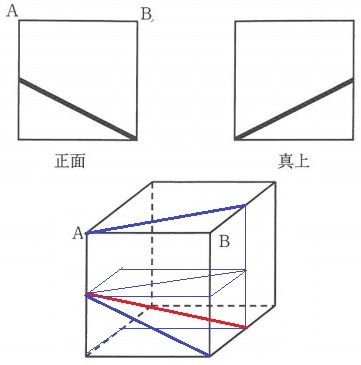
↑赤線が答え。
青い辺が対角線になる長方形を面とする、直方体の対角線。
(7)
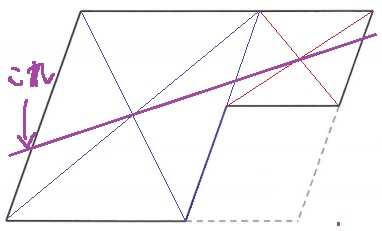
対角線の交点(真ん中)を通る直線は平行四辺形を2等分する。
2つの平行四辺形の真ん中を通過する直線。
@別解@

大きい平行四辺形の半分-小さい平行四辺形の半分で面積が等しくなる。
(8)
3本の切り目で8つに分ける。
ポイントは折り目に接しているところはつながって1枚だが、
折り目に接していないところは上下に2組あらわれる。
(折り目に接していないところの合計は必ず偶数個)
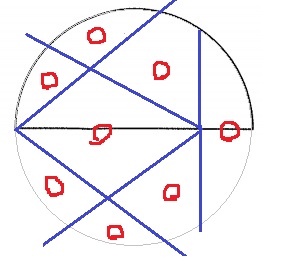
折り目に接しているところが2ヶ所。
(8-2)÷2=3→接していないところを3ヶ所つくる。

折り目に接しているところが4ヶ所。
(8-4)÷2=2→接していないところを2ヶ所つくる。
(10)

A~Dを展開図に書き込む。
数字の向きに気をつけよう!緑の線に向かって書かれる。
イ
(11)①
A定食であれば、A定食のみ、ご飯付き、サラダ付き、ご飯とサラダ付き。
これはB定食とC定食にもいえるので、4×3=12通り
②
350円→A定食(5人)
400円→A定食+ご飯(8人)、B定食(6人)
470円→A定食+サラダ(5人)
520円→A定食+ご飯+サラダ、B定食+サラダ(合計7人)
A定食+ご飯+サラダ以外の情報をまとめる。
350円×5=1750円
400円×8=3200円
470円×5=2350円
18人で合計、1750+3200+2350=7300円
『A定食を注文した人の支払金額の平均は417円』
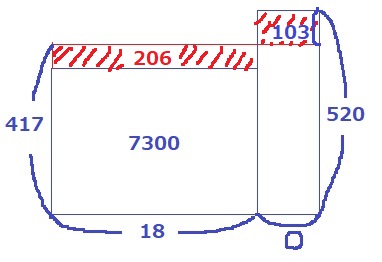
520円でA定食+ご飯+サラダを頼んだ人を〇人とする。
2つの長方形を均すと417円で、赤い長方形は同じ面積になる。
左の赤い長方形が、417×18-7300=206
〇=206÷(520-417)=2人
よって、A定食を頼んだ人は、18+2=20人



コメント