問題PDF
(1)
3/35の分母と分子に同じ整数を加えて約分したところ、8/15だけ大きい分数となりました。
どんな整数を加えましたか。
(2)
何枚かのコインを横一列に並べます。
3枚以上表が連続するところがある並べ方は何通りですか。
次の場合について答えなさい。
(ア)5枚を並べるとき
(イ)6枚を並べるとき
(3)
ひし形ABCDの対角線上に点Eをとったところ、∠BAE=89°、∠ECD=55°となりました。
このとき、ア、イの角度をそれぞれ求めなさい。

(4)
1辺が2cm、6cm、12cmの正方形が図のように並んでいます。
斜線部の面積を求めなさい。ただし、ABとCDは辺上の点Eで交わっています。

(5)

1辺が6cmの立方体をある平面で切断し、真正面、真上、真横から見たところ、
上図のようになりました。この立体の体積を求めなさい。
ただし、角すいの体積は(底面積)×(高さ)÷3です。
@解説@
(1)
先に和を求めよう。
3/35+8/15=65/105=13/21
分母の35と分子の3に同じ整数を加えた=分母分子の差は32で変わらない。
13/21の分母と分子を倍にしていき、分母分子の差が32となる場所を探す。
13/21=26/42=39/63=52/84 ←84-52=32!
分子:52-3=49(分母:84-35=49)
よって、加えた整数は49。
(2)ア
3枚以上が表になる並べ方を調べる。
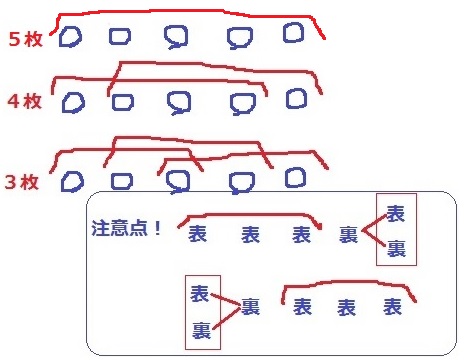
5枚すべてが表→1通り
4枚が連続で表→2通り
3枚が連続で表になる場合、左か右で3連続か、中3つが連続する。
注意点としては、左か右が3連続の場合、反対側のコインは表でも裏でもいい。
○を表、●を裏として左が表3連続だと、○○○●○と○○○●●の2パターンができる。
→計5通り
よって、1+2+5=8通り
イ
6連続→1通り
5連続→左右で2通り
4連続→先ほどの3連続と一緒になる。
左右に4連続が表を配置した場合、隣が裏、その隣はどちらでも可で5通り。
3連続→考え方は同じ。
以下のカッコ内の△は表裏どちらも可とする。
○○○●(△△)→4通り
●○○○●(△)→2通り
(△)●○○○●→2通り
(△△)●○○○→4通り
すべて合計すると20通り。
(3)
Eが対角線BD上にあるということなので、とりあえずBDを書く。
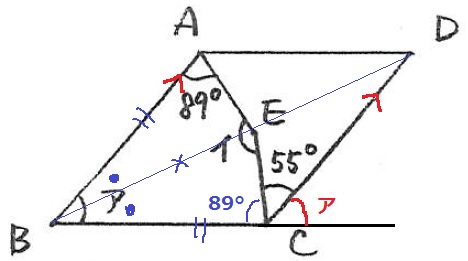
菱形からBA=BC、対角線は∠ABCを2等分するので∠ABE=∠CBE、
共通辺BEより2辺と間の角が等しいので、△ABEと△CBEは合同。
∠BCE=∠BAE=89°
アを同位角で右に移動させる。
ア=180-(89+55)=36°
イ=360-(36+89×2)=146°
@余談@
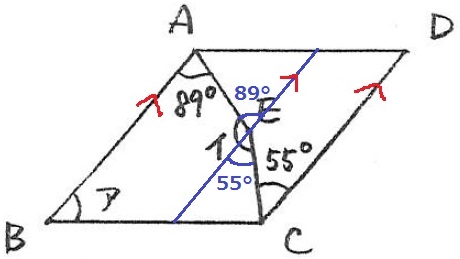
ABとDCに平行な線をもう1本ひくと、直接イを求めにいくことができる。
イ:55+(180-89)=146°
ABCDが菱形でなくとも、平行四辺形であれば使える。
(4)
きちんと方針を立てないと迷う:( ´ω` ):

BDの長さが知りたい。
そこでBDを1辺とする△BDEと相似になる三角形を探す。
→△FCE
CFの長さがが知りたい。FGの長さがわかればいい。
FGを1辺とする△FGAと△BHAの相似から出発する。
FG=12×2/20=1.2cm
FC=6-1.2=4.8cm
△FCEと△BDEは相似だから、BD=4.8×12/6=9.6cm
よって、△BDEの面積は、9.6×12÷2=57.6cm2
(5)
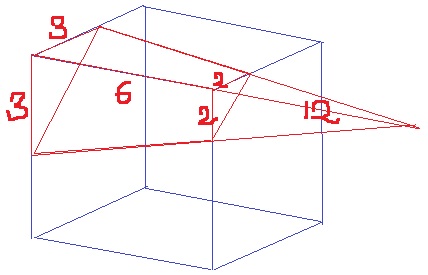
切断部分は三角柱の下。
3×3×3:3×3×3-2×2×2=27:19
求める立体の体積は、6×6×6-3×3×1/2×18×1/3×19/27
=216-19=197cm3



コメント