問題PDF
(大問10個編成、社会と合わせて試験時間50分しかないタイムアタック形式)
【1】(1)

(5)
1×2×3×…のように、1から順に整数をかけていきます。
このとき、かけ算の結果が、6で8回わったときに整数になるのは、
1からいくつまでの整数をかけたときですか。そのうち、最も小さい整数を求めなさい。
(7)
濃度20%の食塩水100gつくるために、水100gに食塩20gをとかしました。
しかし、つくった食塩水が20%でないことに気づいたので、
つくった食塩水を少しすててから食塩を加えて20%の食塩水を100gつくりました。
すてた食塩水は何gですか。
【2】
あるきまりにしたがって、次のように整数が並んでいます。
1、1、2、3、4、2、2、3、4、5、3、3、4、5、6、4、4、5、6、7…
このとき、左から4番目の奇数である3は、はじめから数えて8番目の整数です。
では、左から999番目の奇数は、はじめから数えて何番目の整数ですか。
【3】(1)
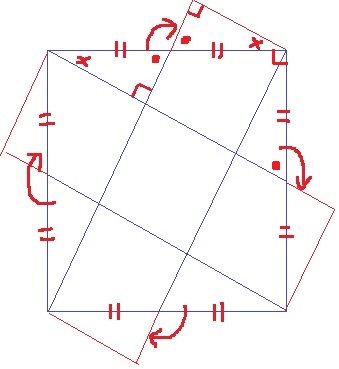
次の図のように、1辺が6cmの正方形の紙を対角線で切り、
対角線が平行になるように重ね合わせました。このとき、斜線部分の面積を求めなさい。

【4】(2)
次の図のような直方体の水そうAとBがあります。
水そうAには12cm、水そうBには5cmの深さまで水が入っています。
Aの水をすべてBに入れると、水の深さは14cmになりました。
その後、水そうAとBの深さが同じになるように、Bの水をAにもどしました。
このときの水の深さを求めなさい。

【5】
正方形を並べてその中に直線をひき、いろいろな模様をつくります。
このとき、各問いに答えなさい。
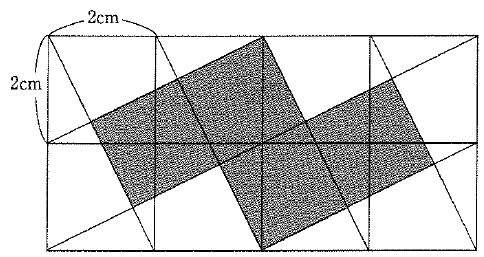
(1)次の図のように、1辺が2cmの正方形を8個並べて直線をひき、模様をつくりました。
このとき、色がぬられた部分の面積を求めなさい。
(2)
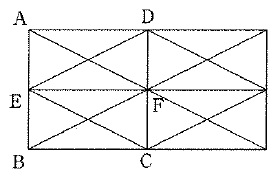
下の図のように正方形ABCDを2つ並べ、AB、CDの中点をE、Fとします。
その中に直線をひくと、長方形やひし形などさまざまな形の四角形を見つけることができます。
例えば長方形に着目すると、下の図のような3種類の長方形を合計7個見つけることができます。
ただし、正方形は除きます。
では、平行四辺形に着目すると、何種類の平行四辺形を合計何個見つけることができますか。
ただし、正方形、ひし形、長方形は除きます。

【6】
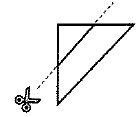
次の図は、正方形の折り紙を三角形になるように3回折ったようすを表したものです。

同じ折り方で、正方形の折り紙を三角形になるように5回折り、
図のようにはさみで切りました。このとき、折り紙は何枚の紙に分かれますか。
【7】
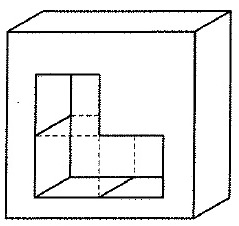
次の図のように、ある木の枠に同じ大きさの立方体を3個つなげて穴をあけました。
この立方体を5個つなげたとき、木の枠を通り抜けることができる立体はどれですか。
下の中からすべて選びなさい。ただし、木の枠を通り抜けている途中では、
立体はひねったり、ずらしたりせず、真っすぐ通り抜けるものとします。

【8】
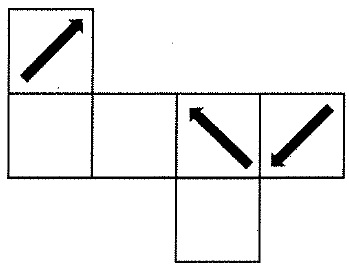
次の図のような立方体の展開図があります。
この展開図を、矢印の書かれた面が表面になるように組み立てました。
組み立てた立方体をいろいろな方向から見たとき、あてはまらないものはどれですか。
下の中からすべて選びなさい。

【9】
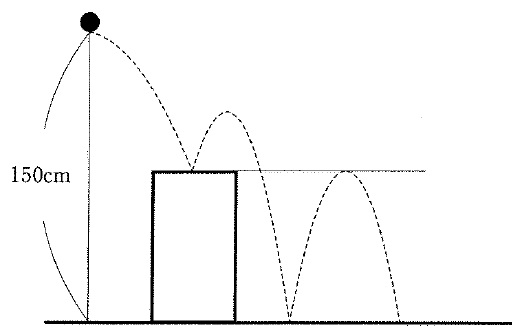
あるボールを地面に落とすとき、そのボールは落とした高さの75%まではね上がります。
次の図のように、地面から150cmの高さから直方体の箱の上で一度はずむようにボールを落としたところ、地面に着いてから直方体の箱と同じ高さまではね上がりました。
また、直方体の箱の上ではねるときは地面ではねるときの2/3までしかはね上がらないことがわかっています。このとき、直方体の箱の高さは何cmですか。
【10】
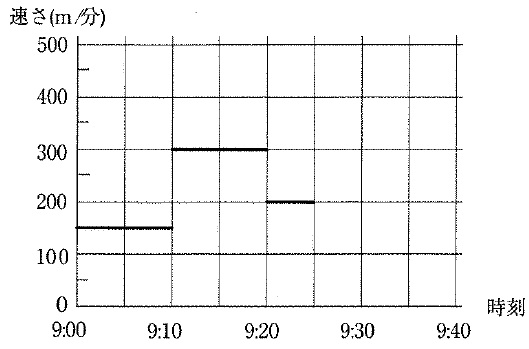
ケンタさんは、9時に家を出て7km離れた駅まで移動したところ、9時40分に駅に到着しました。次のグラフは、時刻とケンタさんの速さを表したもので、9時から9時10分までは分速150mで移動したことが分かります。一方、駅にいた兄のユウトさんは忘れ物をとりに行くために9時5分に駅を出発し、一定の速さで移動し9時40分に家に到着しました。
このとき、下の各問いに答えなさい。
(1)
ケンタさんが9時25分から9時40分まで一定の速さで移動したとき、その速さを求めなさい。
(2)
兄のユウトさんとケンタさんが家から駅まで同じ道のりを移動するとき、
2人がすれちがうのは、9時何分ですか。
@解説@
【1】(1)

パッと見て3.4と34が目に映る⇒分配法則
例)3.4×250=3.4×10×250÷10=34×25

時間がとにかく足りないので分配法則必須です。
(4)

ポイントは24で通分したあと、分母を50にすること。
24と50の最小公倍数600で通分すると分子の範囲が広くなり、
既約分数を数えるのが難しくなる。
9×50/24=18.75
16×50/24=33.33…
18.75<□<33.33…
このなかで50と約分できない数は、
【19・21・23・27・29・31・33】の7個。
(5)
6で8回割ったときに整数になる。
6=2×3
2は偶数でたくさんでてくるので、素因数3が8回でてきたときが答え。
9の倍数は素因数3が2回でてくる。
3・6・9(3×3)・12・15・18(3×3)
よって、18。
(7)

食塩水を捨て、食塩だけ追加する。
ということは、捨てた後の水の量は変わっていない。
ゴールから逆算する。20%食塩水100gの水は80g。
捨てる前の水が100gだから、捨てる前の水:捨てた後の水=100:80=⑤:④
捨てた量は①。
捨てた食塩水は、120×①/⑤=24g
【2】
5個ずつに分ける。
〔1・1・2・3・4〕〔2・2・3・4・5〕〔3・3・4・5・6〕…
999番目の奇数が問われているので、奇数(キ)と偶数(グ)で置き換え、
〔キ・キ・グ・キ・グ・グ・グ・キ・グ・キ〕…と10個ずつのグループにする。
1グループにキは5個。
999÷5=199グループ…4
余りの4は1グループの4個目のキ⇒8番目
10×199+8=1998番目
【3】(1)

対角線が平行になるように重ねるので、直角二等辺三角形がたくさん登場する。
正方形の1辺は6cm、赤い長方形の横の長さは4cmですべての長さを確定する。
赤い長方形から直角二等辺2つ(1辺3cmの正方形)を引けばいい。
4×5-3×3=11cm2
【4】(2)
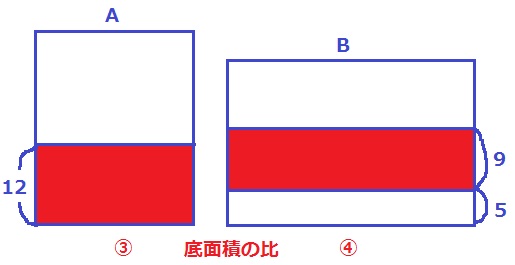
赤い部分の体積が等しい。
高さの比が12:9=4:3なので、底面積は逆比で③:④。
Aに戻してAとBの深さを等しくする→AとBを一体化させて底面積を⑦と考える。
14cm×④/⑦=8cm
【5】(1)
↑これと一緒。
正方形の頂点と辺の中点を結んだ図形で、
●+×=90°と等辺から合同な直角三角形を移すと小さな正方形が5つできる。

全体の面積は4×8=32cm2
今度は小さな正方形に注目し、10個のうちの4個。
32×4/10=64/5cm2
(2)
過不足なく数えなくてはならず、時間が奪われる。
格子状のラインは必ず長方形になってしまうので、斜め線は必ず1本いる。

斜め線+短い辺、斜め線+長い辺、斜め線+斜め線の3種類で12個。
菱形の除外に気をつけよう。
【6】
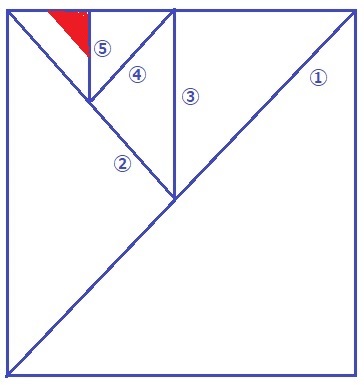
折り目の順番を①~⑤とする。赤い部分が切り落とすところ。
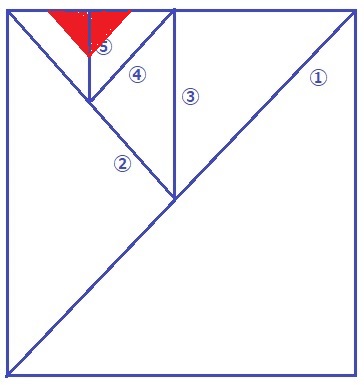
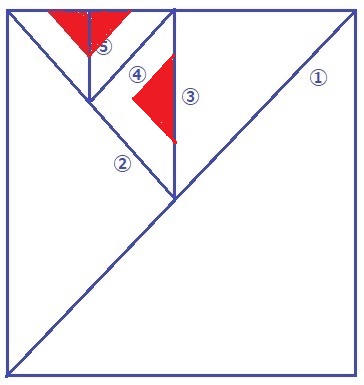
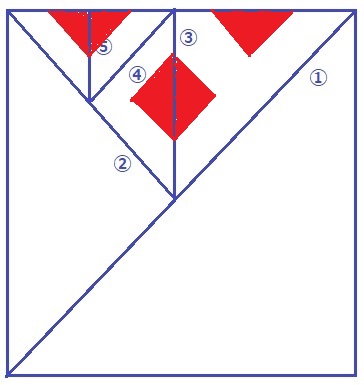
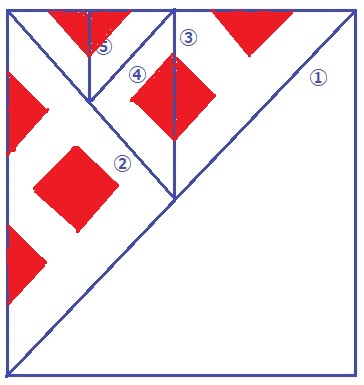
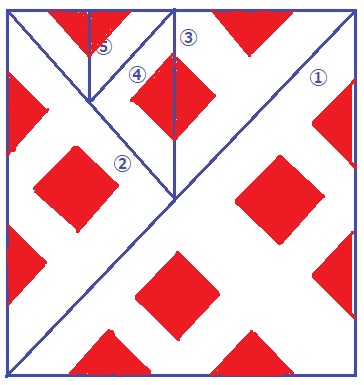
⑤→④→③→②→①と赤い部分を対称移動させていく。
穴が12個+紙1枚で13枚に分かれる。
【7】
thinkthinkという知育アプリにもありました。

L字(or2個or1個)を見つければ終了。
ウ・エ・オ
【8】
すべて式ゆえ時間を消費しやすい。
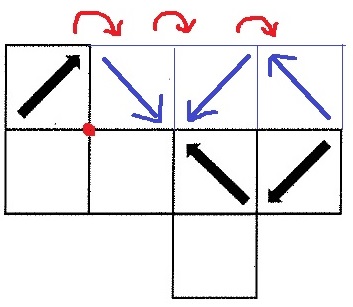
左上の面を赤い点●を中心に時計回りに90°回転させ、右に寄せる。
転がしていくと上のようになる。

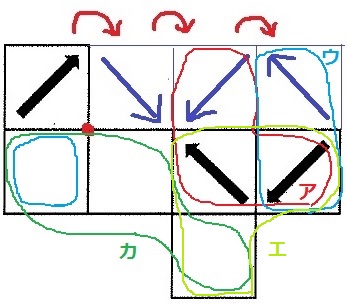
イは矢印の1つが頂点を指し、その頂点から2つの矢印が伸びるが無い。
オが曲者。矢印の面が左右逆だとあるが、オの形は無い。
イ・オ
【9】
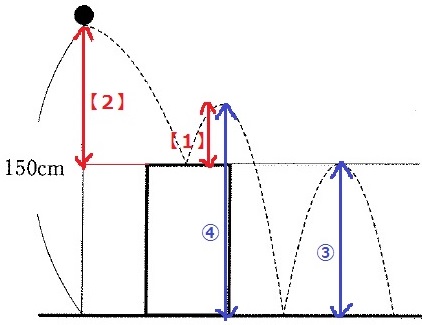
地面からの跳ね返りは75%なので、最後は高さは④→③。
長方形の箱の跳ね返りは75%の2/3倍なので、3/4×2/3=1/2
ボールを落とした地点から箱の上までの高さを【2】とすると、
箱の上では【1】の高さで跳ね返る。
すると、【1】=①となり、そのまま連比で計算できる。
150cm=⑤、箱の高さ=③
150×③/⑤=90cm
【10】(1)

ケンタは変速する。
9:25までに移動した距離を求める。
150×10+300×10+200×5=5500m
残りは、7000-5500=1500m
これを15分で歩くから、1500m÷15分=分速100m
(2)
兄の速さは、7000m÷35分=分速200m
ケンタの移動距離に注意して、どのタイミングで出会うのか確認する。
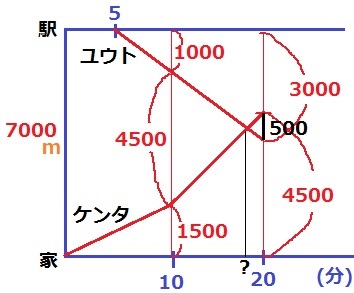
ケンタの出発から10分後、両者の距離は、
7000-150×10-200×5=4500m
20分後の移動距離はケンタ…4500m、ユウト…3000mで7000mを超すので、
10~20分後に出会うことになる。
20分後の両者の距離は、4500+3000-7000=500m
ダイヤグラム上の三角形の相似を活用。
4500:500=9:1
?=10+10×9/10=19分
9時19分




コメント