2021年度　立教新座中学過去問【算数】大問３解説

問題ＰＤＦ
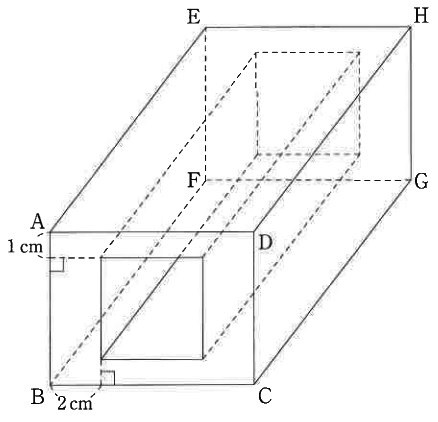
図のように、ＡＢ＝６ｃｍ、ＡＤ＝８ｃｍ、ＡＥ＝12ｃｍの直方体ＡＢＣＤ―ＥＦＧＨから、
１辺の長さが４ｃｍである正方形を底面とする直方体でまっすぐ奥までくりぬいた立体があります。
次の問いに答えなさい。

（１）
この立体の体積と表面積をそれぞれ求めなさい。

（２）
辺ＡＤ、ＢＣ、ＥＨの真ん中の点をそれぞれＰ、Ｑ、Ｒとします。
この立体を３点Ｐ、Ｑ、Ｒを通る平面で切断したとき、点Ａをふくむ方の立体をＫとします。
立体Ｋの表面積を求めなさい。

（３）
（２）の立体Ｋにおいて、辺ＡＥ、ＰＲの真ん中の点をそれぞれＳ、Ｔとし、
辺ＢＦ上にＢＵ＝４ｃｍとなる点Ｕをとります。
立体Ｋを３点Ｓ、Ｔ、Ｕを通る平面で切断したとき、
点Ａをふくむ方の立体の体積を求めなさい。

◆表面積

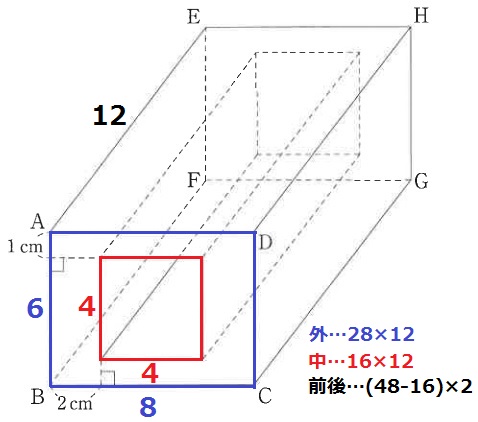
外側を展開すると、横28（長方形ＡＢＣＤの周りの長さ）ｃｍ、縦12ｃｍの長方形。
中側を展開すると、横16ｃｍ、縦12ｃｍの長方形。
これに前後の32ｃｍ²を足す。

28×12＋16×12＋32×２
＝44×12＋64＝592ｃｍ²

（２）

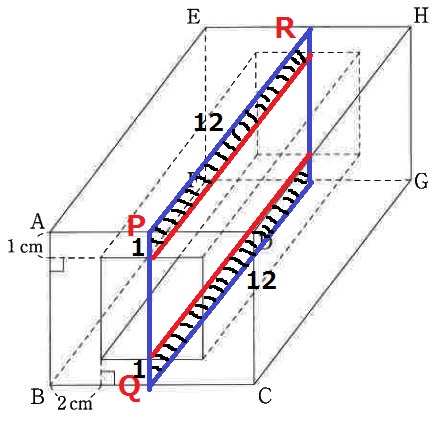
外・中・前後は前問の半分。
切断により新たにむき出しになる部分は、うえの斜線部分。
592÷２＋２×12＝320ｃｍ²

（３）

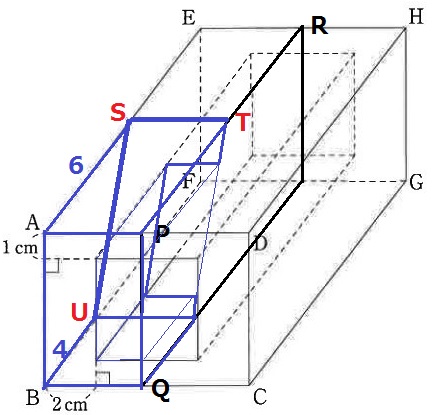
断面の形はコ。
立体Ｋは全体の半分だから、384÷２＝192ｃｍ³

四角形ＡＢＦＥで捉える。
断面はコの字だが、一様にコの字なので柱体の切断とみなし、上底＋下底の比が使える。
全体の体積比は、12＋12＝㉔
求積すべき立体の体積比は、６＋４＝⑩
192×⑩/㉔＝80ｃｍ³
難関中（算数科）解説ページに戻る