問題ＰＤＦ
２から100までの数字が書かれたカードをそれぞれ10枚ずつ、合計990枚あります。
このカードを使って、次の＜ルール１＞で数を作ります。
＜ルール１＞
カードを何枚か選び、そのカードに書かれた数字をすべてかけて数を作る。
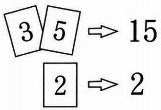
例えば、【３】のカード１枚と【５】のカード１枚を選んだとき、できる数は15になり、
【２】のカード１枚だけを選んだとき、できる数は２になります。
（１）
数12の作り方は全部で〔 〕通りあり、数49の作り方は全部で〔 〕通りあります。
次に、＜ルール１＞に＜ルール２＞も合わせて数を作ります。
＜ルール２＞
＜ルール１＞で数を作るとき、カードをできるだけ多く選んで作る。
例えば、数18を作るとき、
１枚のカードで作ると、【18】のカード１枚です。
２枚のカードで作ると、【２】のカード１枚と【９】のカード１枚または、
【３】のカード１枚と【６】のカード１枚です。
３枚のカードで作ると、【２】のカード１枚と【３】のカード２枚です。
しかし、４枚以上のカードでは、数18を作ることはできません。
したがって、数18を作るときは、
「【２】のカード１枚と【３】のカード２枚の合計３枚のカードを選んで作ります」です。
今、＜ルール２＞で、２から100までの数を作ることを考えます。
（２）
数30を作るとき、〔 〕枚のカードを選んで作ります。
（３）
カードを４枚使って作ることができる数は全部で〔 〕個あります。
（４）
使うカードが最も多い枚数でできる数をすべて求めると〔 〕です。
このとき、使うカードの枚数は〔 〕枚です。
最後に、＜ルール２＞で作った２から100までの数を＜ルール３＞で作りかえます。
＜ルール３＞
＜ルール２＞で２から100までの数を作った後、選んだカードに同じカードがあれば、２枚ごとにそのカードを捨てる。こうして手元に残ったカードに書かれた数字をすべてかけて、あらためて数を作り直す。ただし、すべてのカードを捨てて、手元にカードがなくなったときは、かけてできる数は０とする。
例えば、＜ルール２＞で数18は、【２】のカード１枚と【３】のカード２枚の合計３枚のカードで作っているので、【３】のカードを２枚捨てると、手元に残ったのは【２】のカード１枚だけです。よって、作り直してできる数は２です。
また、＜ウール２＞で数９は、【３】のカード２枚だけで作っているので、
手元のカードはすべてなくなります。よって、作り直してできる数は０です。
（５）
＜ルール３＞で、２から100までの数をすべて作り直しました。
このときできる数は、全部で〔 〕種類です。
＠解説＠
（１）
【12】、【２】×【６】、【３】×【４】、【２】×【２】×【３】
４通り。
【49】、【７】×【７】
２通り。
（２）
カードの枚数を多くして30を作る。
30を素数だけの積で表す→素因数分解！
【２】×【３】×【５】
３枚
（３）
最小の数である【２】の枚数で場合分けするのが良いかな？
２×２×２×２＝16、３×３×３×３＝81
【３】が４枚で81だから、そんなにないはず。
ポイントは素数のカードを選択すること。
前問と同様で素数に分解できる合成数は、もっとカードを増やせるのでＮＧ。×
◆【２】が４枚
〔２・２・２・２〕
◆【２】が３枚
〔２・２・２・３〕
〔２・２・２・５〕
〔２・２・２・７〕
〔２・２・２・11〕
積が100を超さないように！
８×□≦100
◆【２】が２枚
〔２・２・３・３〕
〔２・２・３・５〕
〔２・２・３・７〕
〔２・２・５・５〕
小さい素数から入れ替えて慎重に調べる。
◆【２】が１枚
〔２・３・３・３〕
〔２・３・３・５〕
◆【２】が０枚
〔３・３・３・３〕
以上、12個。
（４）
最も小さい素数【２】のベキ乗を想像する。
２×２×２×２×２×２＝64
２の７乗＝128で100over。×
また、最後の２を３に変えて、
２×２×２×２×２×３＝96
64と96
カードの枚数は６枚。
（５）
同じカードを２枚ずつペアで取っていく。
→同じ素数が２つある数はなくなって作り直される。
作り直された数は、なくなった素数２個を除いた素数の積だから既出。
たとえば、問題文の例題で挙げられる18ならば、２×３×３→２で２は既出。
同じ素数が２つある数を見つけ、全体から引けばいい。
【２】×【２】→４の倍数
【３】×【３】→９の倍数
【５】×【５】→25の倍数
【７】×【７】→49の倍数
【11】×【11】…100overゆえ×！
49の倍数は49と98の２個しかなく、４の倍数でも９の倍数でも25の倍数でもない。
また、25の倍数は25・50・75・100。
このうち100は４の倍数と重複するから、３個でカウントしておく。
残りは、１～100までの４の倍数と９の倍数の個数を求める。
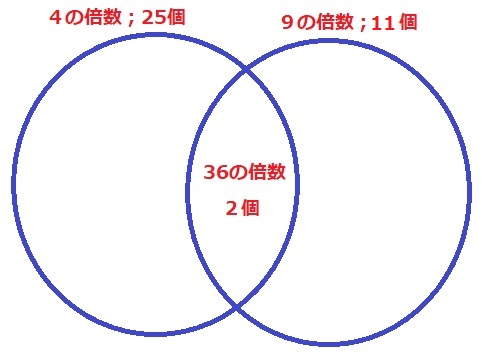
ベン図処理。
25＋11－２＝34個
１～100で４の倍数・９の倍数・25の倍数・49の倍数は、２＋３＋34＝39個
100－39＝61個
留意点は、手元のカードがすべてなくなると０ができること。
さらに、【１】のカードはないので１は作ることができない。
61＋１－１＝61個
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
ああああああああああ」
お試し投稿でしょうか？(;^ω^)