問題ＰＤＦ
次の①～③のルールにしたがって整数をつくって、左から右へ順番に並べていきます。
＜ルール＞
①１番目の数を０とする。
②２番目の数をａとする。（ａは１けたの整数とする。）
③３番目からあとの数は、１つ前につくった数と２つ前につくった数を
たした数の１の位の数とする。
このルールで整数を並べたときのｎ番目の数を、（ａ、ｎ）と表します。
たとえば、ａ＝１とすると、数が０、１、１、２、３、５、８、３…と並ぶので、
（１、８）＝３となります。次の各問いに答えなさい。
（１）
（１、ｎ）＝０にあてはまるｎのうち、２番目に小さい数を求めなさい。
（２）
（１、2023）＋（ａ、2023）＝10にあてはまるａをすべて求めなさい。
＠解説＠
（１）
ａ＝１は０を付けたフィボナッチ数列である。
最初はフィボナッチの一の位を書き上げて調べる。
【０、１、１、２、３、５、８、３、１、４、５、９、４、３、７、０】
２番目の０は16番目。
ｎ＝16
（２）
規則を探るために続きを書いてみる。
16番目が０なので、15個ずつに区切ると、
【０、１、１、２、３、５、８、３、１、４、５、９、４、３、７】
【０、７、７、４、１、５、６、１、７、８、５、３、８、１、９】０…
１列目と２列目の数字は異なるが、31番目にまた０がでてくる。
２列目は077…からスタートなので、問題文に照らし合わせるとａ＝７の数列である。
もう１列＋α調べると規則が見つかるかもしれない。
ａ＝１【０、１、１、２、３、５、８、３、１、４、５、９、４、３、７】
ａ＝７【０、７、７、４、１、５、６、１、７、８、５、３、８、１、９】
ａ＝９【０、９、９、８、７、５、２、７、９、６、５、１、６、７、３】
ａ＝３【０、３、３、６、９、５…】
ここらで気が付きたい。
１列目はすべて０、２列目は1793、３列目は1793でａの値と一緒。
数列を横ではなく縦読みするのでは？
１列目が１→７→９→３、５列目は３→１→７→９…８列目は３→１→７、９列目は１→７→９…？
１の位に着目した数列で、１→７→９→３→１→７→９→３→１…??
ここまでくれば見えやすいと思う。
７の倍数の１の位が循環している。
（*７×１＝７、７×７＝49、49×７＝343、343×７＝2401）
１行15個なので、2023÷15＝134…13
横の数列で2023は13列目にあたる。
先の法則に従えば、13列目は４→８→６→２がループする。
今度は縦の数列に切り替えると、2023は135行目にあたるので、
135÷４＝33…３から、（１、2023）＝６となる。
ということは、（ａ、2023）＝４
13列目は４→８→６→２の繰り返しで、余り３が2023にあたるから、
３番目が４となるように調整すると〔６→２→４→８〕
１行目13列目が６になるのはａ＝９
残りは１・３・７・９以外にある。
ａ＝１【０、１、１、２、３、５、８、３、１、４、５、９、４、３、７】
ａ＝７【０、７、７、４、１、５、６、１、７、８、５、３、８、１、９】
ａ＝１を７倍した１桁がａ＝７の数列だった。
つまり、ａ＝１を２倍した１桁の数列がａ＝２、３倍した１桁の数列がａ＝３の数列になる。
解説ページなので全部書いてみました。１の位だけで計算してみましょう。
ａ＝２はａ＝１の２倍。ａ＝８はａ＝２の４倍。
ａ＝７の２倍はａ＝14ですが、14→４とするとａ＝４と符合します。
ａ＝１の全体の数列の2023番目が６なので、各々の2023番目の一の位は、
ａ＝２…６×２＝12→２×
ａ＝４…６×４＝24→４〇
ａ＝５…６×５＝30→０×
ａ＝６…６×６＝36→６×
ａ＝８…８×６＝48→８×
したがって、ａ＝４・９
＠余談＠
フィボナッチ数列の一の位は、この60個の数を１周期としてループすることになる。
フィボナッチ数列の2023番目の一の位は、2023÷60＝33…43
45番目は３行目の最後の３なので、43番目は６。
数値の配列が線対称でも点対称でもないくせに、この収まり具合はいったい何なのだろう…。
フィボナッチ数列っていろんな性質を持つと聞きましたが、こんなのもあったんですね(´ﾟωﾟ`;)
ａ＝１→７→９→３の繰り返しで、７倍した数の一の位が縦に連なることになりますが、
この理由をご存知の方がいましたらコメント欄かお問い合わせよりお知らせ願います。
＠＠
＞フィボナッチ数列と有限体（Ikuro’s Home Page）
こちらのページにそれっぽいのがありました。
【２】フィボナッチ数の周期性のところです。
ある数の１の位は、その数を10で割ったときの余りの数に等しいので、
ある数ｍ（mod）で割って余りが周期する長さを調べていくと、
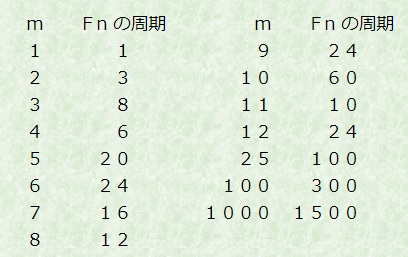
例えば、それぞれのフィボナッチ数を÷３（mod3）した余りを調べると、
〔０、１、１、２、０、２、２、１〕の８個がループします。
÷４（mod4）では〔１、１、２、３、１、０〕の６個です。
頑張って計算していけば、mod10の周期が60、mod100が300、mod1000が1500となるので、
下１桁の周期は60個、下２桁は300個、下３桁は1500個だそうです。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント