問題PDF
(1)
(7×3.5+7×0.8-7×2.3)÷0.25を計算しなさい。
(3)
( )にあてはまる数を求めなさい。
容器Aには濃度6%の食塩水が300g、容器Bには濃度( )%の食塩水が500g入っています。
Aから200gの食塩水をくみ出し、Bに入れてよくかきまぜます。
次にBから200gの食塩水をくみ出し、Aに入れてよくかきまぜます。
Aの食塩水の濃度は5.2%になりました。
(4)
下の図で、AC:AD=4:7のとき、BC:CDを求めなさい。

(5)
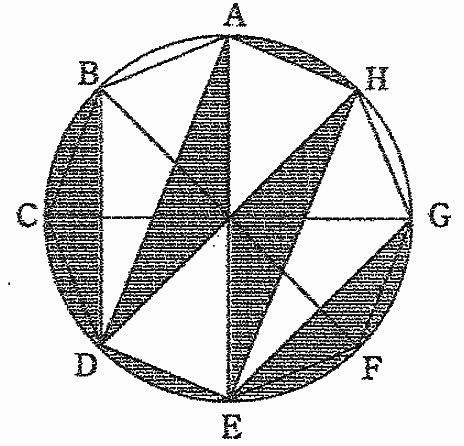
下の図は、半径12cmの円で、点A~Hは円周を8等分する点です。
色のついた部分の面積を求めなさい。
(6)
1辺10cmの立方体の3つの面の外側に、底面の半径4cmで高さ2cmの円柱を、
立方体の面から底面の円がはみ出ないように1つずつくっつけます。
できた立体の表面積を求めなさい。
(7)
( )にあてはまる数を求めなさい。
100人の生徒にお正月に何をしたか質問したところ、
おせち料理を食べた人は98人
百人一首をした人は65人
たこあげをした人は72人
もちつきをした人は80人でした。
4つ全てをした人は( )人以上( )以下と考えられます。
@解説@
(1)
分配法則。
(7×3.5+7×0.8-7×2.3)÷0.25
=7×(3.5+0.8-2.3)×4
=56
(2)
分子を10で統一する。
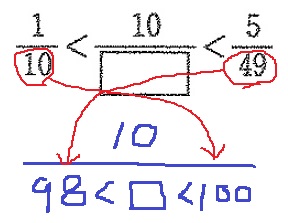
分子を統一すると、分母の大小関係は逆になる!
□=99
(3)
食塩水の交換は中学受験で頻出だが情報整理が苦しい。
うしろから攻めよう。
最後のAは濃度5.2%、食塩水300g→食塩の量は、300×5.2%=15.6g
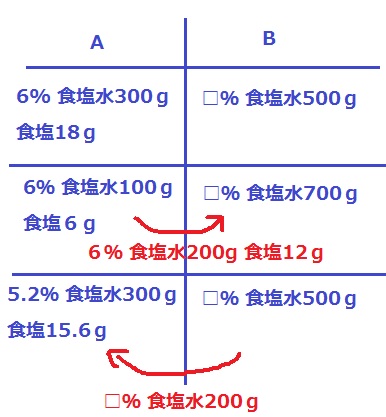
B→Aに渡った食塩は、Aの食塩の増加分から15.6-6=9.6g
その濃度は、9.6/200=4.8/100=4.8%
Aの一部を混ぜた後のBの濃度は4.8%となる。

Aの一部を混ぜる前のBの濃度を求めたい。
お馴染みの天秤法。

支点からの距離は2:5
□=4.8-1.2×2/5=4.8-0.48=4.32%
(4)
角度の数字を活用する。
〔180-77-26=77〕
反対側に77°をつくると一直線になる!

DAを延長。△ABCと合同な△ABEを作成。
AE=AC=④
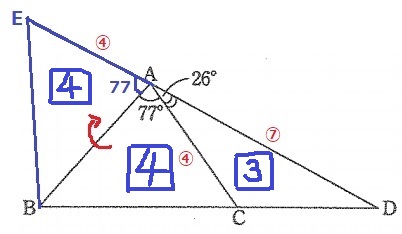
△ABCの面積を【4】とする。
合同で△ABEは【4】
EA:AD=△ABE:△ABD→△ABD=【7】
△ACD=【7】-【4】=【3】
BC:CD=△ABC:△ACD=4:3
@別解@
YAさんから素晴らしい解法を頂きました。

AC=AE=④となるように、AD上にEをとります。
△ACEは二等辺ゆえ、∠ACE=(180-26)÷2=77°
∠BAC=∠ECA=77°より、錯角が等しいのでABとECが平行です。
平行線と線分の比から、AE:ED=BC:CD=4:3
(5)
長方形は特別な平行四辺形で、対角線がおのおのの中点で交わる。
対角線で長方形は4等分される。
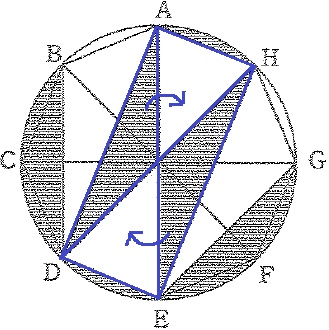
長方形ADEHの内部の三角形を隣に移動。
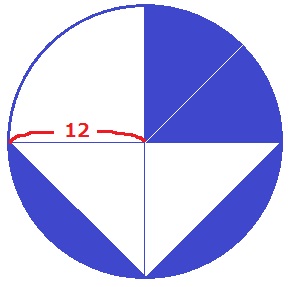
さらに場所を入れ替えると、4分の3円から直角二等辺をひいた図形になる。
12×12×3.14×3/4-24×12÷2
=339.12-144=195.12cm2
(6)
文章から立体を想像する。
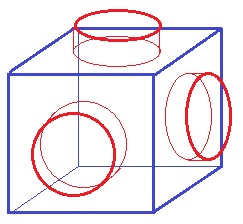
立方体の表面積に円柱の側面積を足せばいい。
10×10×6+4×2×3.14×2×3
=600+150.72=750.72cm2
(7)
4つ全てをした人の最小値と最大値を求める。
■最大値■
最も多いおせちを食べた98人の中に、百人一首、たこあげ、もちつきを押し込む。
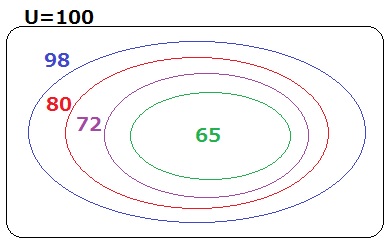
集合の包含関係。4つ全てをした人は一番真ん中の65人。
■最小値■

おせち98人と、もちつき80人の両方をした人を最も少なくしたい場合、
ベン図で98と80の枠を左右に離す。(ダブらせないように配置する)
両方やった人は、98+80-100=78人
この78人と、たこあげ72人を同様に計算して両方した人を少なくすると、
78+72-100=50人
百人一首も同様。
50+65-100=15人
よって、15人以上65人以下。
@最小値の別解@
やっていない人から考えることもできる。
おせち食べてない人→2人
百人一首やってない人→35人
たこあげしてない人→28人
もちつけしてない人→20人
これらを重ならないように配置すると、
2+35+28+20=85人
100人以下なので重ならない。
4つのやってないに触れないところは、100-85=15人




コメント