問題PDF
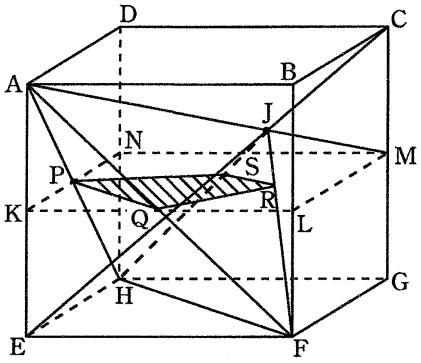
AB=24cm、AD=18cm、AE=24cmの直方体ABCD―EFGHがあり、
辺AE、BF、CG、DHの真ん中の点をそれぞれK、L、M、Nとします。
また、CEとAMの交点をJとします。
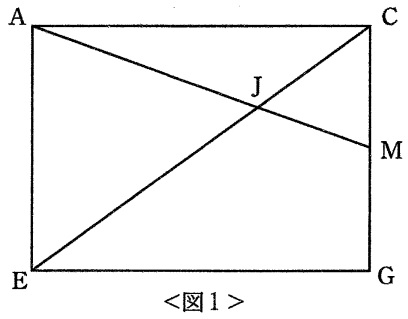
<図1>は四角形AEGCをぬき出したものです。
(1)
EJ:JCを最も簡単な整数の比で表しなさい。
また、底面をEFGHとしたとき、点Jの高さは何cmですか。
(2)
長方形KLMNとAH、AF、JF、JHとの交点をそれぞれP、Q、R、Sとします。
①PQ、SRの長さはそれぞれ何cmですか。
②四角形PQRSの面積は何cm2ですか。
@解説@
(1)

断面図が提供されている。
△AEJと△MCJが相似。
EJ:JC=2:1
24cmの高さの比を③とすると、Jの高さの比は②に相当する。
Jの高さ…24×②/③=16cm
(2)①
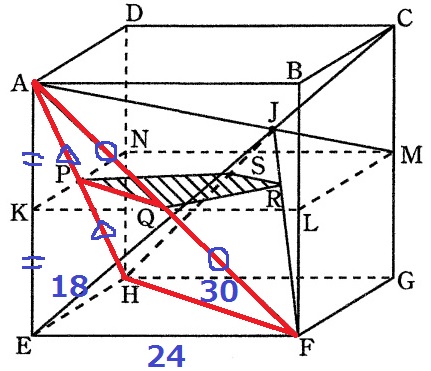
PQを1辺とする三角形は△APQ。
PQが含まれる面KLMNは面EFGHと平行→PQとHFも平行。
△APQと△AHFの相似比は1:2。HFの長さがわかればいい。
算数の範囲で解ける直角三角形の斜辺の長さは有名三角形に限られる。
△HEFの辺の比を調べると3:4:5だから、HF=30cm
PQ=30÷2=15cm
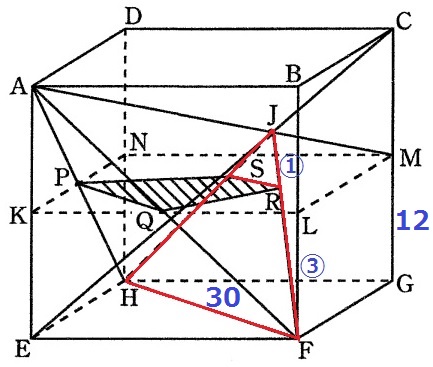
同様に△JSRと△JHFが相似。
先ほどJの高さは16cmと出している。
SとRの高さは12cmだから、高さの比から相似比は△JSR:△JHF=①:④
SR=30×①/④=7.5cm
答え…PQ=15cm、SR=7.5cm
②
出しづらい:;(∩´_`∩);:
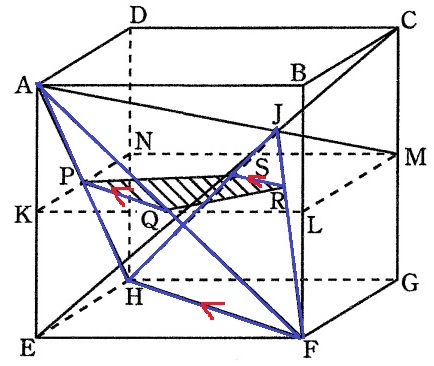
(<は平行線の印)
PQとHFが平行、SRとHFが平行ということは、HFを媒介にPQとSRも平行である。
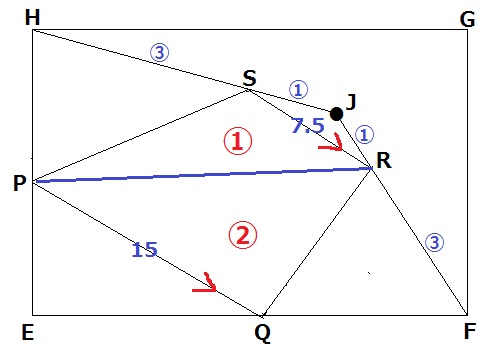
上から見た図を作成。(長方形の頂点は便宜上、EFGHを打ちました)
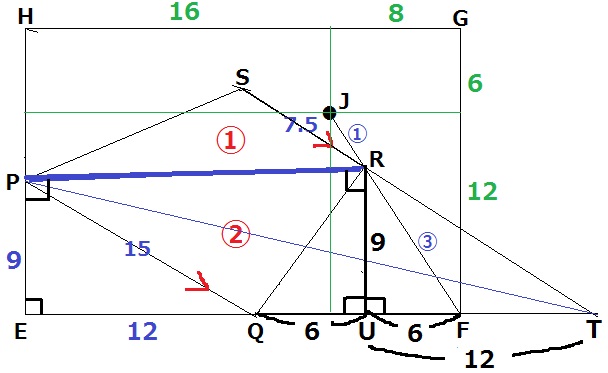
前問の図より、JR:RF=①:③
上底SRの2倍がちょうど下底PQなので、△PRS:△PQR=①:②
△PQRの面積を3/2倍すれば台形PQRSになる。
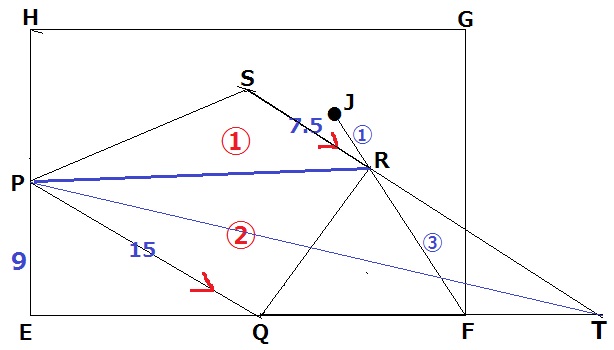
SRとEFを延長した交点をTとする。△PQRと△PQTは等積である。
△PQTの高さはPE=9cm。底辺QTさえわかればいい。

S・Rの位置はJに由来するので、Jから考える。
(1)のEJ:JC=2:1は直方体の対角線。
この斜め線の比は縦方向と横方向を内分する比と同じである。
上図は緑の数字でJの位置を特定した。
Rの垂線の足をUとする。JR:RF=①:③を用いて、
RU=12×③/④=9cm
UF=8×③/④=6cm
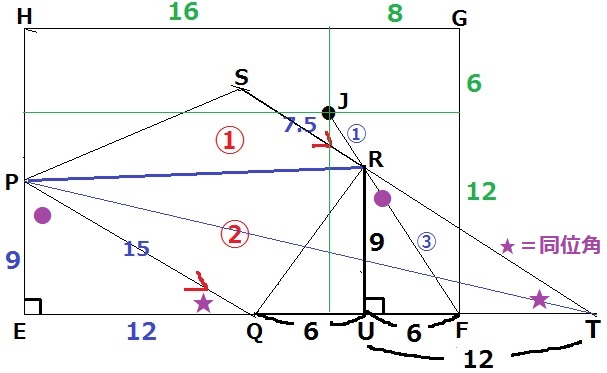
QF=12cmだから、QU=12-6=6cm
△PEQと△RUTに着目すると、斜辺が平行でPE=RUの直角三角形→合同(1辺両端角)
UT=EQ=12cm
QT=6+12=18cm
したがって、18×9÷2×③/②=121.5cm2
@別解@
歪んじゃいましたが、PE=RU=9cmということは四角形PEURは長方形です。
△PQRは長方形の半分である点からも、18×9÷2×3/2の式が導けます。



コメント