問題ＰＤＦ
３以上の整数Ａ、Ｂを用いて、次の操作を行います。
①１辺の長さがＡｃｍである正Ｂ角形を作り、頂点と、頂点から各辺上に１ｃｍごとに点を打ちます。正Ｂ角形のすべての頂点に黒い石を置きます。
②次の手順（ⅰ）、（ⅱ）を交互に繰り返し、残り全ての点の上に黒か白の石を１つずつ置いていきます。ただし、すでに石が置いてある点には新しい石は置きません。
（ⅰ）黒い石のとなりにあるすべての点の上に白い石を置きます。
（ⅱ）白い石のとなりにあるすべての点の上に黒い石を置きます。
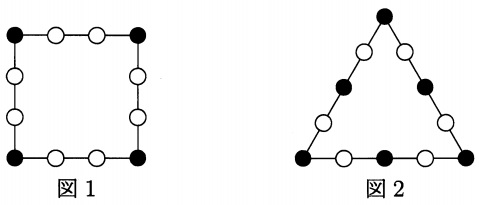
たとえば、図１は、Ａ＝３、Ｂ＝４のときで、置いた黒い石の数は４、置いた白い石の数は８です。また、図２は、Ａ＝４、Ｂ＝３のときで、置いた黒い石の数は６、置いた白い石の数は６です。次の問いに答えなさい。
（１）
Ａ＝５、Ｂ＝７とするとき、黒い石の数と白い石の数はそれぞれいくつですか。
（２）
白い石の数が15のとき、考えられるＡの値を全て書きなさい。
（３）
黒い石の数が24のとき、考えられるＡの値は何通りありますか。
＠解説＠
（１）
Ｂ＝７ゆえ、正七角形。
Ａ＝５→１辺に６つの点が打たれる。
両サイドは正七角形の頂点なので黒を置く。
中に向かって白、黒…と配置するとうえのようになる。
魔方陣の要領で考えると、１つのグループの中に黒は３つ、白は２つ。
黒…３×７＝21個
白…２×７＝14個
（２）
魔方陣で考えると、各グループに含まれる白の数は同じで、その合計が15個。
グループの数＝正Ｂ角形の辺の数、すなわち、Ｂの値は15の約数である。
もっとも、多角形は三角形以上なのでＢ≧３
◆Ｂ＝15
白は15÷15＝１個
●〇●
Ａ＝２
◆Ｂ＝５
白は15÷５＝３個
●〇●〇●〇●
Ａ＝６
◆Ｂ＝３
１つのグループに白は15÷３＝５個
●〇●〇●〇●〇●〇●
Ａ＝10
したがって、Ａ＝２、６、10
（３）
ここも魔方陣で考える。
グループの数は24の約数で、かつ３以上。
Ｂ＝24・12・８・６・４・３
◆Ｂ＝24
１グループに黒の数は１個。
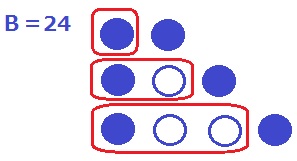
調べてみると、黒と黒のあいだに白が０・１・２個あるかで３パターンある。
Ａ＝１～３
◆Ｂ＝12
１グループに黒は２個。
こちらはＡ＝４しかない。
つまり、１グループの黒の個数が奇数だと３パターン、偶数だと１パターンとなる。
◆Ｂ＝８
１グループに黒は３個。
奇数だから３パターン（Ａ＝５～７）
◆Ｂ＝６
１グループに黒は４個。
偶数だから１パターン（Ａ＝８）
◆Ｂ＝４
黒は６個。Ａ＝12
◆Ｂ＝３
黒は８個で、Ａ＝16
したがって、Ａの値は10通り。
難関中（算数科）解説ページに戻る
コメント