問題ＰＤＦ
各位の数字がすべて異なる３けたの９の倍数について、次の問いに答えなさい。
（１）
数字の９が入っているものは何通りできますか。
（２）
各位の数の和が18であるものは何通りできますか。
（３）
各位の数の和が９であるものは何通りできますか。
（４）
数字の２が入っているものをすべて足したとき、その和はいくつですか。
＠解説＠
（１）
９の倍数→位の和が９の倍数
３桁の数字はすべて異なる。
（９・８・１）（９・７・２）
（９・６・３）（９・５・４）
各組み合わせのなかで順番を入れ替えると、３×２×１＝６通り
６×４＝24通り
（２）
和を18にする。
◆９＋○＋○
前問から24通り。
◆８＋○＋○
（８・７・３）（８・６・４）
６×２＝12通り
◆７＋○＋○
（７・６・５）
６通り
これ以上はない。
よって、24＋12＋６＝42通り
（３）
和を９にする。
◆０を含まない
（１・２・６）（１・３・５）（２・３・４）
６×３＝18通り
◆０を含む
（０・１・８）（０・２・７）（０・３・６）（０・４・５）
０は百の位にはなれないので、各々２×２×１＝４通り
４×４＝16通り
よって、18＋16＝34通り
（４）
和が27以上の組み合わせはないので、前問までにでてきた組み合わせのなかで、
２が登場するものをピックアップする。
和が18→（９・７・２）
和が９→（１・２・６）（２・３・４）（０・２・７）
（９・７・２）の場合、279＋297＋729＋792＋927＋972となる。
各位では２と７と９が２回ずつ登場することに注目！
（２＋７＋９）×２＝36
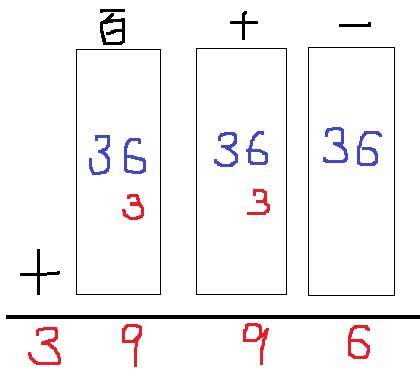
（１・２・６）（２・３・４）を筆算すると各位の和が18となり、
うえのように計算すると、おのおの3996となる。
（０・２・７）→207＋270＋720＋702＝1899
3996＋3996＋1899＝9891
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント