問題PDF
頌子さんと栄子さんは、遠くに立っている瓶をボールを転がして倒すゲームをしました。

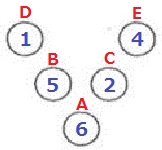
下の表1は頌子さんの得点表と、その回が終了したときの瓶の状態を表した図です。

次の問いに答えなさい。
(1)
A~Eの瓶の点数を求めなさい。
(2)
1回戦から10回戦まで全て![]() だった場合の得点を求めなさい。
だった場合の得点を求めなさい。
(3)
下の表2は栄子さんの5回戦までの得点表ですが、
一部の点数が汚れで見えなくなってしまっています。

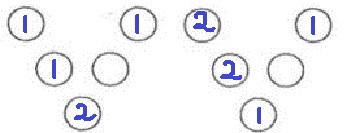
5回戦の1投目で倒した瓶を①、5回戦の2投目で倒した瓶を②とし、
5回戦で倒した瓶の組み合わせを全て求め、解答用紙の図に書き込みなさい。

例えば、1投目にA、2投目にCとEを倒した場合は、図1のように書きます。
解答用紙の図を全て使うとは限りません。
@解説@
ボーリングだけど…ルールが少し変わっている。
(1)
A~Eの瓶の得点をあてる。ここを間違えるとすべて間違えるので必答です。
4回戦までの得点から推論できる。

1回戦:A+C=8
2回戦:BorD→1or5
3回戦:B+C+D=8(どれかが2)
4回戦:DorE→1or4
2回戦と4回戦で共通するD=1
B=5、E=4となる。
3回戦より、C=8-(5+1)=2
1回戦より、A=8-2=6
A…6点、B…5点、C…2点、D…1点、E…4点
(2)
![]() の処理を正確に!
の処理を正確に!
すべて瓶を倒した場合(以下ストライクとする)
『直後の2投の合計点数をその回の得点に加える』
ストライクを出した回はA~Eの和である18点。
表1の5回戦は18点に6回戦の1点と4点が加わり、18+1+4=23点
『5回までの合計得点』(累積)で27+23=50点となる。
1回戦~10回戦まですべてストライクであった場合、
1回戦は18点に2回戦と3回戦の18点を足して18×3=54点
2回戦は18点に3回戦と4回戦の18点を足して18×3=54点
3回戦も同様に4回戦、5回戦の分を足して54点
…
9回戦は10回戦の1投目と2投目を足して54点
10回戦はルール(オ)より、18×3=54点
したがって、54×10=540点
3回戦はストライク。直後の2投は4回戦の2投ですべての瓶を倒した(以下スペアとする)
ということは、3回戦のストライク18点に4回戦(直後の2投)の18点を加算して、
3回戦の得点は18+18=36点
3回戦までの累積→17+36=53点
4回戦はスペアなので、5回戦の1投目が加点される。
5回戦の1投目をA点、2投目をB点とする。
4回戦の得点は、累積点の差から81-53=28点
18(4回戦のスペア)+A=28
A=10
同様に、5回戦の得点は累積点の差から97-81=16点
18点未満なのでスペアではない!
10+B=16
B=6点



コメント