問題PDF
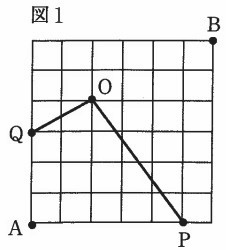
1cmの目盛りの工作用紙を、1辺が6cmの正方形の形に切り出して、図1のように3点O、A、Bをとります。さらにこの正方形の周上に2点P、QをとりOからPまでと、OからQまでをまっすぐカッターで切ります。
(1)
点P、Qが図1の場合、切りはなされた2つの部分のうち小さい方の面積を求めなさい。
以下、問い(2)、(3)、(4)では分けられた2つの部分のうち、小さい方の面積が常に10cm2となるように切りはなすこととします。P、Qの位置は線の交差している場所でなくてもかまいません。
(2)、(3)の答え方は、点Aから右または上に何cm、点Bから下または左に何cmとします。例えば、図1の点Qは「点Aから上に3cm」、図3の点Pは「点Bから左に5cm」となります。点Aや点Bに一致するときは「点Aから×に0cm」のように答えなさい。

(2)
点Pが図2の位置にあるとき、点Qの位置として考えられる点をすべて答えなさい。
(3)
点Pが図3の位置にあるとき、点Qの位置として考えられる点をすべて答えなさい。
(4)
点Pから点Qに正方形の周上を反時計回りにたどった方が時計回りにたどるよりも距離が短いように点P、Qを決めます。また、点P、Qは異なる辺に含まれるものとします。
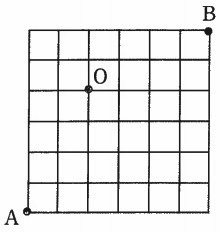
点Pを含む辺と辺Qを含む辺が隣り合わないのは、点Pがどこにあるときですか。あり得る場所の範囲を解答らんの図に太線で表しなさい。なお、正方形の頂点については考えなくてもかまいません。
@解説@
(1)
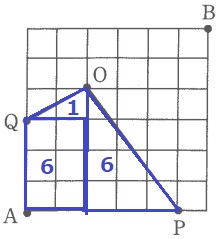
13cm2
(2)
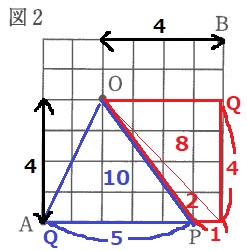
Pの左と右に10cm2の領域をつくる。
正方形の辺とOの距離がともに4cmなので、
Pから底辺の合計が5cmとなる場所がQになる。
点Aから×に0cm、点Bから下に2cm。
(3)
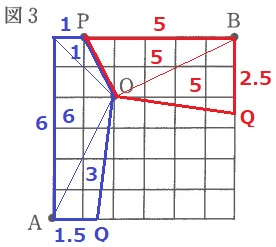
同様にPの左と右に10cm2の領域を作成。
高さに気を付けながら10cm2になるまで底辺を増やしていく。
点Aから右に1.5cm、点Bから下に2.5cm。
(4)
Pの反時計回りにQがいる。
『PとQは異なる辺に含まれるものとする』『Pを含む辺とQを含む辺が隣り合わない』
→PとQは正方形の対辺にある(なお、問題文から正方形の頂点は考えなくてよい)
面積10cm2を維持しながら、PとQが正方形の対辺にくるときのPの範囲を調べる。

①PはAからスタート、ここからPとQを反時計回りに辺上を移動させる。
高さ(O~正方形の辺までの距離)は4cmだから底辺の合計は5cm。
②QがBに到着。ここまでは高さが4cmなので、底辺の合計は5cmのまま。
PとQは対辺にない。
③Qが左上の頂点に到着。ここから先はPとQが対辺にくる。
④PがBに到着。対辺でなくなる。
⑤QがAに到着。これ以降は対辺の関係。
⑥Pが左上の頂点に到着。対辺でなくなる→①に戻る。
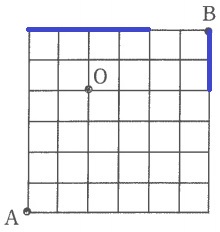
↑解答



コメント