2018年度　早稲田実業学校中等部過去問【算数】大問２解説

問題ＰＤＦ
一辺の長さが９ｃｍで、表が白色、裏が黒色の正方形の折り紙ＡＢＣＤがあります。
点Ｐを折り紙の上にとり、頂点Ａが点Ｐに重なるように折って、
図１のように黒い図形を作ります。
次の各問いに答えなさい。

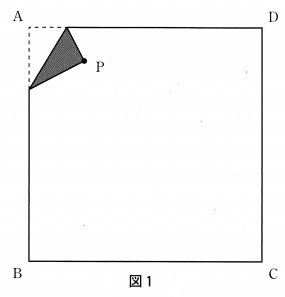
（１）
図２のように点Ｐを正方形の対角線ＡＣ上にとり、黒い図形を作ったところ、
黒い図形の面積と表の面積の比が１：２になりました。ＡＰの長さを求めなさい。

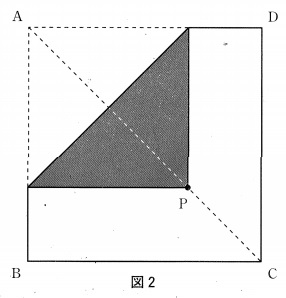
（２）
図３のように点ＰをＤＰ＝３ｃｍとなるように辺ＣＤ上にとり、
黒い図形を作ったところ、ＤＱ＝４ｃｍとなりました。黒い図形の面積を求めなさい。

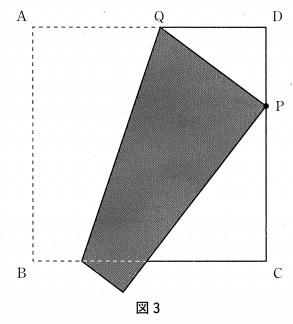
（３）
頂点Ａから点Ｐを出発させ、黒い図形が三角形になるに点Ｐを動かします。
点Ｐの動ける範囲を解答欄の図に斜線で示しなさい。

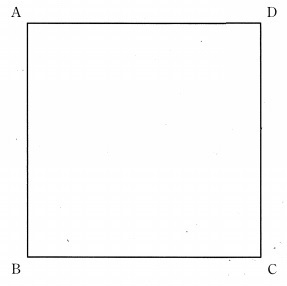
＠解説＠
（１）

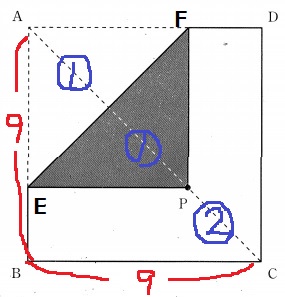
Ｐは対角線上の点⇒四角形ＡＥＰＦは正方形。
正方形全体④＝81ｃｍ²
正方形ＡＥＰＦ②＝81÷２＝81/２ｃｍ²
ＡＰは正方形ＡＥＰＦの対角線。ＡＰ＝□とおくと、
□×□÷２＝81/２
□＝９→ＡＰ＝９ｃｍ

（２）
問題集でも見かける形ゆえ、正解したい。

黒い図形は台形なので、上底と下底の長さが知りたい。

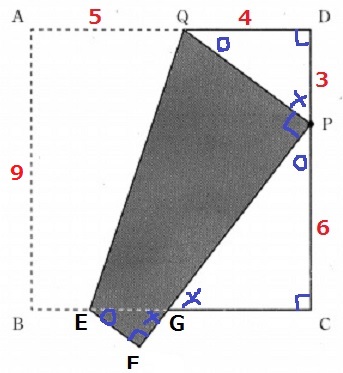
○＋×＝90°として直角三角形の角度を調査
→２角が等しく、３つの相似図形がでてくる。
直角三角形ＱＤＰに注目すると、辺の比が３：４：５！

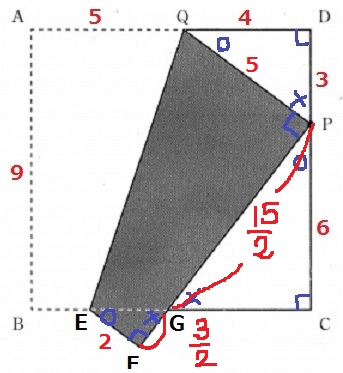
ＰＧ＝６×５/４＝15/２ｃｍ
ＧＦ＝ＰＦ－ＰＧ＝９－15/２＝３/２ｃｍ
ＥＦ＝３/２×４/３＝２ｃｍ
よって、（２＋５）×９÷２＝63/２ｃｍ²

（３）

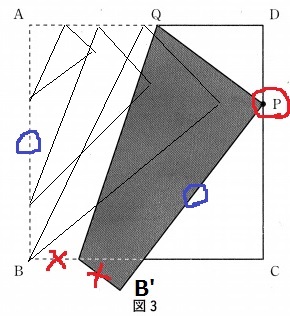
辺ＡＢ上にできる折り目の一端に注目。
折り目の端がＢを超えると、黒い図形が三角形から四角形に変わる。
同様のことは辺ＡＤにも言える。（折り目の端がＤを超えるとＮＧ！）

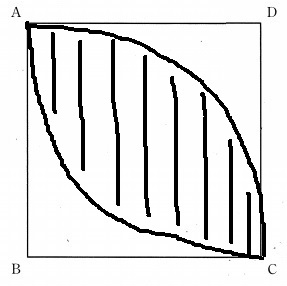
折り目の一端が辺ＡＢか辺ＡＤから離れないような点Ｐの範囲を作図する。
ＡＢ・ＡＤを半径とする４分の１円を描き、
これらの弧より外側だと折り目の一端がいずれかの辺から離れ、黒い図形が四角形になるので、
その内部のラグビーボールが正解。
難関中（算数科）解説ページに戻る