問題PDF
あきこさんは、神奈川県の箱根町に住む祖母から「寄木細工」の工作キットを送ってもらい、お母さんといっしょに作ることにしました。この工作キットには、図1、図2、図3の3種類のひし形の部品がたくさん入っていました。それぞれの部品は大きさが等しく、内側の角度が60°と120°になっています。

あきこさんのお母さんは、図1の部品を3枚、図2の部品を3枚、図3の部品を6枚の合計12枚を使って、図4のコースターを作りました。図4のコースターの各部品に、図5のとおりアからシまでの記号をつけて、あきこさんとお母さんが【会話】をしています。

【会話】
お母さん:私が作ったコースター、きれいなデザインでしょ。
あきこさん:そうね。あれ、ちょっと待って。規則的になっていないところがあるよ。
お母さん:あ、本当だ。でも、まだ接着剤を付けていないから直せるよ。どう直そうかしら。
あきこさん:直す方法にはいろいろあるね。
例えば、お母さんが作ったコースターは、①キの部分を1回だけ動かせば、
対称の軸で折ると②色や模様がぴったり重なる線対称な図形に変えられるよ。
お母さん:ありがとう。風車のように見えるわ。
あきこさん:風車といえば回転するよね。③色や模様がぴったり重なる点対称な図形もできるかな。
(注) コースター:コップなどの下にしく平たい物。
このとき、次の各問に答えなさい。
問1
下線部①について、どのように動かすと下線部②の線対称な図形になるか、
次の【条件】にしたがって動かし方を説明しなさい。

問2
下線部②について、お母さんが作った図4のコースターを、下線部①の動かし方をして
下線部②の線対称な図形に変えたとき、その図形の対称の軸の本数を答えなさい。
問3
下線部③について、お母さんが使った12枚の部品をすべて使って、
下線部③の点対称な図形を作ることはできるでしょうか。
「できる」ならば、できあがった点対称な図形をかきなさい。
「できない」ならば、その理由を説明しなさい。

@解説@
(1)

しま模様を横向きにしたい。
しかし、回転させても横向きではフィットしない。
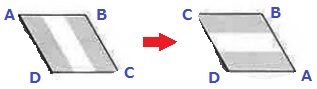
しま模様は辺AD、辺BCに対して平行である。
頂点AとCをひっくり返すようにうら返すと、辺AD、辺BCが横向きになり、
しま模様も横向きになる。
(2)
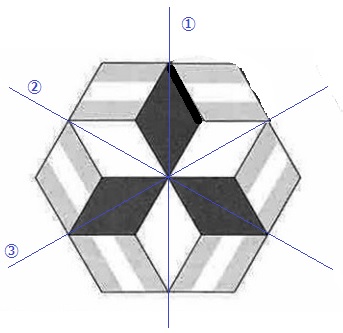
正六角形の対称の軸は6本。
このうち、黒と白の部品が対称関係になるのは3本。
(3)
できない。

点対称は回転の中心に対し、各パーツの位置関係や向きが対称的でなければならない。
黒と白のパーツはおのおの3個。奇数個だと基本的に対称的な位置関係に置けない。
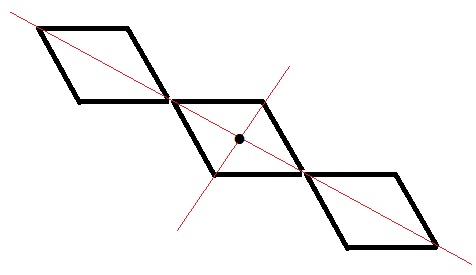
奇数個でもうえのように中央のパーツが点対称の位置にあれば良いが、
本問は真ん中に置けないので点対称は無理。



コメント