問題ＰＤＦ
ＡさんとＢさんの姉妹２人が家から学校に向かい、学校に着くとすぐに帰ります。２人は同時に家を出発し、Ａさんが３ｋｍ進む間に、Ｂさんは家から学校までの距離の３分の１を進みました。その後、２人とも速さを変えずに進み、Ａさんの方がＢさんより10分早く学校に着きました。
帰りは、Ａさんは同じ速さで進み、Ｂさんは行きの1.5倍の速さで進んだところ、２人は同時に家に着きました。このとき、次の各問いに答えなさい。
（１）
Ｂさんが家に着いたとき、Ａさんは家から何ｋｍ離れた地点にいましたか。
（２）
Ｂさんの行きの速さは時速何ｋｍでしたか。
＠解説＠
（１）
Ａが３ｋｍ進んだときに、Ｂは家～学校間の１/３を進んだ。
ということは、Ｂが学校に着いたときには、
Ｂより速いＡは学校を折り返して３×３＝９ｋｍ進んでいる。
一方、Ｂさんの帰りは行きの1.5倍速なので、行きと帰りの時間の比は1.5：１＝③：②
この③：②の時間の比をＡに照らし合わせると、Ａは③の時間で９ｋｍ進んだことになる。
求めたいのは②の距離なので、９×②/③＝６ｋｍ
（２）
時間の情報が〔10分〕しか与えれていないので、
Ａが学校に着いたとき、Ｂは学校から何ｋｍ手前にいたかに狙いを絞る。
Ａの進んだ距離から家～学校の往復距離は、９＋６＝15ｋｍ
片道は、15÷２＝7.5ｋｍ
Ａが３ｋｍ進むとき、Ｂは7.5÷３＝2.5ｋｍ進んだことになる。
言い換えれば、Ａが３ｋｍ進むうちに、ＡとＢは0.5ｋｍの差が開く。
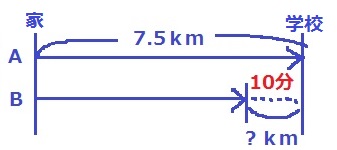
Ａが学校に着いたとき、ＡとＢの差は0.5×7.5/３＝1.25ｋｍ
Ｂは10分で1.25ｋｍ進むので、１時間では1.25×６＝7.5ｋｍ進む。
時速7.5ｋｍ
難関中（算数科）解説ページに戻る
コメント