問題ＰＤＦ
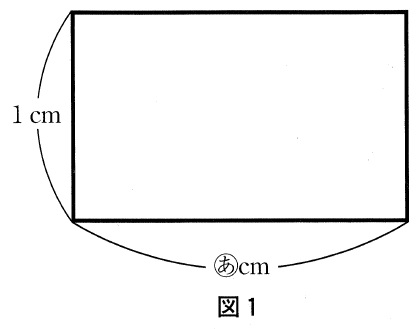
図１のような、縦の長さが１ｃｍ、横の長さが（あ）の長方形の紙があります。
ただし、（あ）は１より大きい数とします。
この紙を縦または横に１回真っすぐ切って、長方形から正方形に切り離します。
残った紙が正方形でなければ再び同じように正方形を切り離し、
残った紙が正方形になるまでこの作業をくり返します。
たとえば、（あ）が２・１/２のときの切り方は、図２のように①縦→②縦→③横となり、
切る回数は３回です。次の各問いに答えなさい。
（１）
（あ）が１・１/４のときの切る回数を求めなさい。
（２）
切る回数が３回となる（あ）の値をすべて求めなさい。
ただし、２・１/２は除きます。
＠解説＠
（１）
最初は１ｃｍで縦に切り、１/４ｃｍで横３回。
切る回数は４回。
（２）
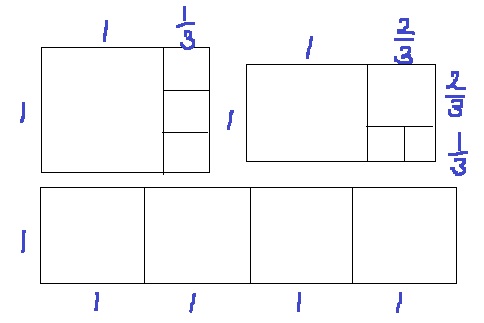
先に切るべきラインを決めてから、横の長さを算出する。
最も小さい辺を①とおいて、すべての辺を○で表し、
１ｃｍが○いくつかを出してから、最後に横を求めると出しやすい。
４/３ｃｍ、５/３ｃｍ、４ｃｍ。
（３）
試しに少しだけ調べてみよう。
切り方は縦、横、縦、横…。
５/３は前問で答えている。４つ目まで調べると何かが見えてくる…。
２を２/１にして数字を眺めてみると、
１・２・３・５・８…前２つの和が連なるフィボナッチ数列！
分母→分子の順で、分子が次の分母にくる。これを10回かけ合わせて144。
＠黄金比＠
縦と横の比が１：（１＋√５）/２（1.618…）は、幾何学的に美しいとされる黄金比。
黄金比は『１辺がａの正方形と、縦がｂ、横がａ＋ｂの長方形の面積が等しくしたときのａ：ｂ』
ｂ＝１とすると、ａ2（正方形の面積）＝ａ＋１（長方形の面積）となり、
これをａについて解くと、ａ＝（１＋√５）/２（1.618…）となる。
フィボナッチ数列で隣り合う２つの数の比の値を並べていくと、
１/１＝１、２/１＝２、３/２＝1.5、５/３＝1.66…、８/５＝1.6、13/８＝1.62…と、
次第に黄金比へ収束されていく。
黄金比はパルテノン神殿やミロのビーナスなどの建築やアートにも使われており、
自然界のいたるところにも登場するという。
VERDADMODAより。縦１：横（１＋√５）/２の長方形から、
本問のように長方形の長い辺を１辺とする正方形を螺旋状に切り出していき、
４分の１円の弧で連続させるとオウム貝になる。
例のロゴもそうだったとは…(;`ω´)
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント