2019年度　女子学院中学過去問【算数】大問１解説

問題ＰＤＦ
（１）

（２）
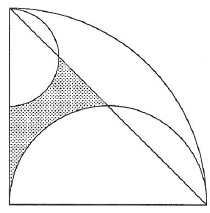
図のように、半径８ｃｍ、中心角90°のおうぎ形の中に
半径４ｃｍの半円と、半径２ｃｍの半円があります。
影をつけた部分の面積は何ｃｍ²ですか。

（３）
ある数Ｘの逆数を、〔Ｘ〕で表すとします。
たとえば、〔３〕＝１/３、〔0.25〕＝４です。
ＡとＢを求めなさい。

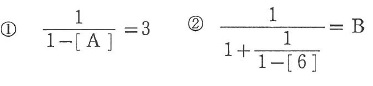
（４）
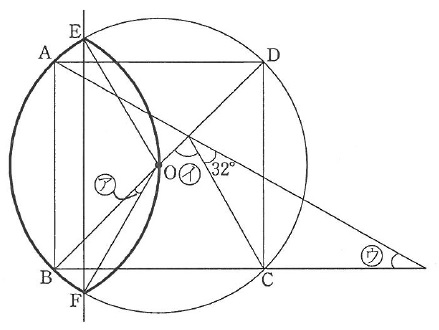
図の四角形ＡＢＣＤは正方形で、点Ｏは円の中心です。
辺ＡＢと直線ＥＦは平行です。太線の図形は、直線ＥＦを対称の軸とした線対称な図形です。

（５）
赤、青、白の３つの円柱の形をした積み木があります。底面積は３つも同じです。
赤の高さは白より５ｃｍ高く、青の上に白をのせたものと赤の高さの差は、
青の高さの３/５です。青の高さは何ｃｍまたは何ｃｍですか。

（１）
しょっぱなから骨が折れる(；^ω^)

ぶつ切りで計算してＯＫ。
７/37＋２/185＝37/185＝１/５
0.18÷１・２/25＝１/６
0.5－１/６－１/673
＝１/３－１/673
＝（673－３）/（673×３）
＝670/（673×３）

１/５×670/（673×３）
＝134/2019
結局、分母は約分できず…。2019は今年ですね。（134は何??）
最後の分数計算で一気に約分できる場合もあるので、かけ算を保留しておくのも手です。

（２）

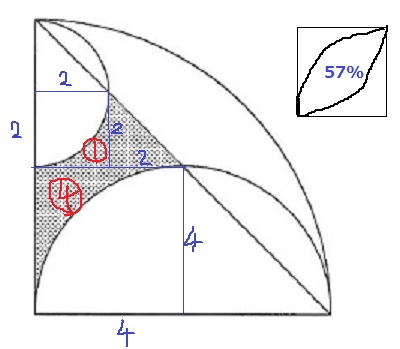
８ｃｍの直角三角形から、４分の１円と直角三角形を２つずつ引いてもＯＫですが、
ここでは足し算でいきます。
円周率が3.14の場合、正方形の中のラグビーボールは正方形の５７％。
残りは４３％でその半分をすればいい。
４×４×43/100÷２＝3.44…④
同じ形の相似形は面積比が４：１→①…3.44÷４＝0.86
3.44＋0.86＋２×２÷２＝6.3ｃｍ²

（３）

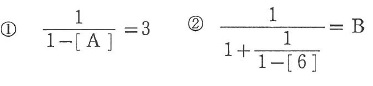
①逆数の約束記号。実体は分数の操作。

分母・分子は同じ数を割っても値は同じ。
１－〔Ａ〕＝１/３
上のように処理して、Ａ＝３/２

②連分数の処理。
分母・分数に同じ数をかけても同じ値。

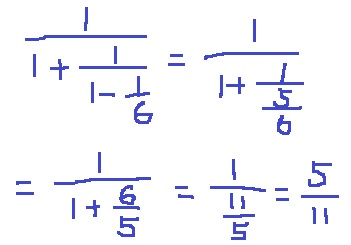
（４）
対角線ＡＣをひいておく。
『太線の図形はＥＦを対称の軸として線対称の図形』を用いる。

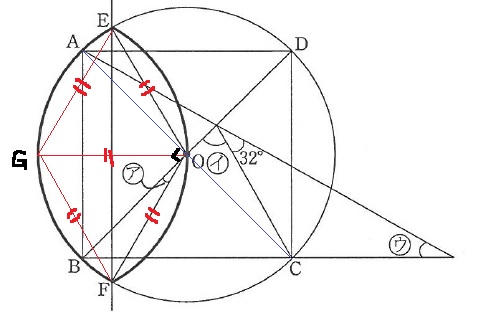
Ｏと対称となる、円周上の点をＧとおく。
半径ＯＥ＝ＧＥ。半径ＯＦ＝ＧＦ
ＯＧは半径だから、△ＥＧＯと△ＦＧＯは正三角形となる。
∠ＥＯＧ＝∠ＦＯＧ＝６０°

ピックアップ。
ＡＣとＢＤは正方形の対角線だから、∠ＡＯＢ＝９０°
ア…（120－90）÷２＝１５°

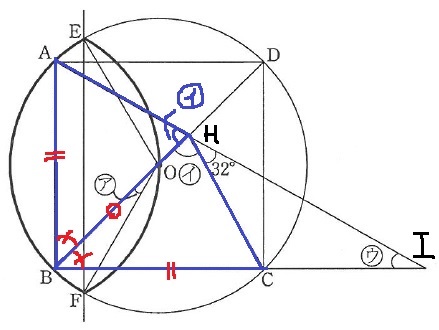
△ＡＢＨと△ＣＢＨに注目！
ＡＢ＝ＣＢ（正方形の１辺）
ＢＤが対角線だから、∠ＡＢＨ＝∠ＣＢＨ＝４５°
ＢＨが共通辺。→２辺と間の角が等しいから、△ＡＢＨ≡△ＣＢＨ
イ…（180－32）÷２＝７４°
△ＨＢＩに注目。
ウ…180－（32＋74＋45）＝２９°

（５）
線分図で情報処理。赤 / 白＋青で区別する。
パターンが２つある。

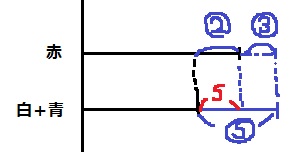
白＋青が赤より長い場合。⑤が青の長さ。
５×５/２＝２５/２ｃｍ

もう１つは、白＋青をしても赤の方が長い場合。
５×５/８＝２５/８ｃｍ
難関中（算数科）解説ページに戻る