問題PDF
(1)
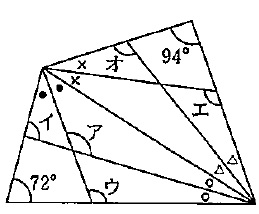
下の図において、印●、○、△、×のついた角はそれぞれ同じ大きさです。
角アの大きさは〔 〕度、角イ、ウ、エ、オの大きさの和は〔 〕度です。
(2)
10=1+2+3+4なので、和が10となる4つの連続する整数の中で一番小さい数は1で、
一番大きい数は4です。和が1000となる最も多くの連続する整数の中で、
一番小さい数は〔 〕で、一番大きい数は〔 〕です。
@解説@
(1)
■アの角度

72+●×2+○×2=180°
(●+○)×2=108°
●+○=54°
角アを含む三角形に注目。
ア=180-(●+○)=180-54=126°
■角イ、ウ、エ、オの大きさの和
四角形全体から、
360-(72+94)=194°…●●××○○△△
●×○△…194÷2=97°
角イウエオそれぞれを1つの角とする4つの三角形に注目。
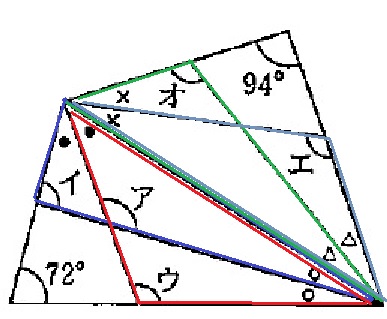
イ●●○+ウ●○○+エ×△△+オ××△
=イ+ウ+エ+オ+(●○×△)×3=180×4=720°
●○×△=97°なので、
イ+ウ+エ+オ=720-97×3=429°
@別解@
外角定理でもいける。

〇+72=イ
●+72=ウ
×+94=エ
△+94=オ
イ+ウ+エ+オ
=〇+●+×+△+72+72+94+94
=97+72×2+94×2=429°
(2)
連続する整数の個数は、奇数個と偶数個に分かれる。
たとえば、1+2+3+4+5=15は連続する5つの整数。
真ん中の3を中心に(2、4)(1、5)と和が同じ組み合わせが登場する。
奇数個では真ん中の数字が基準となる。
たとえば、1+2+3+4=10は連続する4つの整数。
(2、3)(1、4)と和が同じ組み合わせができる。
偶数パターンでは真ん中の数字がなく、組み合わせのみ。
連続する整数を棒グラフで描くと階段状になり、奇数個では平らに均すことができる。
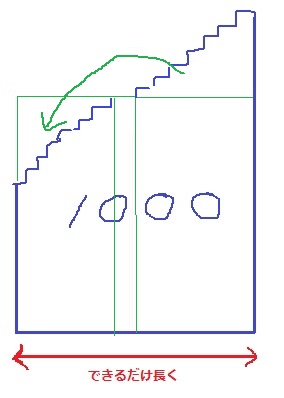
階段の面積が1000になる。横幅が段数。
連続する整数の個数を最も多くするので、段数はできるだけ増やす。
平均の考えで、右上の階段を左下にあてはめれば全体で四角形ができる。
四角形の面積は縦×横→2数の積〇×〇で表される。
横が奇数個なので、偶数×奇数か奇数×奇数である。
一方、偶数個の場合だとうまく均せない。
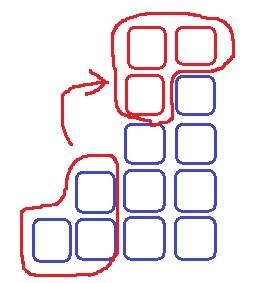
もっとも、こうすると四角形にはできるので○×○の形にはできる。
また、四角形に変形したとき、横が偶数でも縦の長さは必ず奇数になる。
なぜなら、中央にある2つの整数は連続した整数で、その和は奇数だから。
(3・4・5・6であれば、4+5=3+6は奇数)
ということは、○×○で偶数×偶数はない。
○×○=1000の組み合わせをピックアップ。
1×1000、2×500、4×250、5×200、8×125、10×100、20×50、25×40
このうち、偶数×偶数を除外すると、1×1000、5×200、8×125、25×40のみ。
1×1000は、連続する横1000段の整数で、縦1の長さの四角形はできない。
5×200は、200を中央にして連続する5つの整数〔198、199、200、201、202〕で和が1000。
8×125は、(62・63)を真ん中のペアにし、連続する8つの整数〔55~70〕で和が1000。
5と8が極端に少ない数字なので、勘のイイ人は〔25×40〕でないかと推測できると思う。
〔25×40〕の組み合わせで、横に40段並べると縦が25。
段数が偶数個なので、真ん中をのペアが(12・13)となるが、
12から下へ19段目はマイナスになってしまうので不適×。
よって、横の段数を25にする。
奇数個なので、真ん中の数が40。
40、(39、41)、(38、42)、(37、43)…
40から上に12段(=(25-1)÷2)、下に12段となり、
一番小さい数は28、一番大きい数は52となる。



コメント