2020年度　東京都市大学付属中学校過去問【算数】大問２解説

問題ＰＤＦ
Ａ地点からＢ地点までの道のりは2500ｍです。
太郎君はＡ地点から、兄はＢ地点から同時に出発し、一定の速さでＡＢ間を何回か往復します。
（太郎君が走る速さ）：（兄が走る速さ）＝２：３で、
Ａ地点、Ｂ地点に着いてからすぐに引き返すものとして、あとの問いに答えなさい。

問１
出発してから太郎君と兄が１回目に出会うのは、Ａ地点から何ｍのところですか。

問２
出発してから太郎君と兄が２回目に出会うのは、Ａ地点から何ｍのところですか。

問３
太郎君が２回往復するまで兄が走り続けるとき、
兄が太郎君と出会った回数と追いついた回数の合計は何回ですか。

＠解説＠
（１）

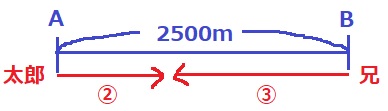
速さと距離は比例。
Ａ地点からの距離②は、2500ｍ×２/５＝1000ｍ

（２）
太郎が1000ｍ歩くと、兄は1500ｍ歩く。
太郎はＢまで残り1500ｍ、兄はＡまで残り1000ｍなので、
太郎と兄が２回目に出会うのは、太郎と兄がＵターンしたあと。

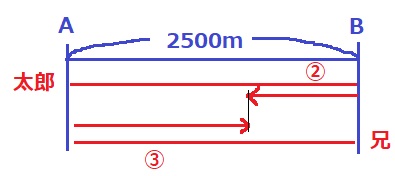
２人が歩いた合計は、2500×３＝7500ｍ
兄が歩いた距離③は、7500×３/５＝4500ｍ
Ａ地点からの距離は、4500－2500＝2000ｍ

（３）
距離と速さの比のみで、速さと時間がわかっていない。
そこで、速さの比をうまく活用する。

速さと距離は比例関係。
速さ②の太郎がＡＢ間を２往復したということは、
速さ③の兄はＡＢ間を３往復したことになる！

太郎は片道４回、兄は片道６回歩くので、
４と６の最小公倍数12分でフィニッシュすると仮定する。

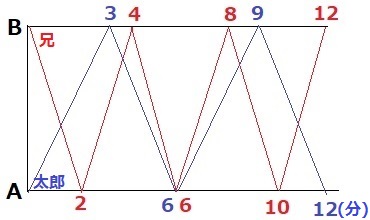
太郎は３分→６分→９分→12分でＡ地点、
兄は２分→４分→６分→８分→10分→12分でＢ地点に戻る。
グラフの交点が出会ったor追いついたとき。
５回
難関中（算数科）解説ページに戻る