問題PDF
図1のように直方体の水そうが、長方形の2つのア、イでP、Q、Rの3つの部分に分けられています。水そうの底面は水平であり、仕切りは水そうの左右の面に平行です。Pの底面には一定の割合で水を排出する排水口があります。また蛇口からは水が一定の割合でQの部分に注がれます。容器や仕切りの厚さは考えないものとします。
排水口を閉じた状態で空の水そうに水を入れたとき、水を入れ始めてからのRの部分の水面の高さと時間の関係は図2のようになりました。
また、排水口を閉じた状態で空の水そうに水を入れ始め、水を入れ始めてから3分30秒後に排水口を開き、その3分12分後に再び排水口を閉じたところ、水を入れ始めてからのPの部分の水面の高さと時間の関係は図3のようになりました。

(1)
(あ)の長さは何cmですか。
(2)
蛇口から出る水は毎秒何cm3ですか。
(3)
排水口から出る水は毎秒何cm3ですか。
@解説@
(1)
(あ)はQの横の長さ。
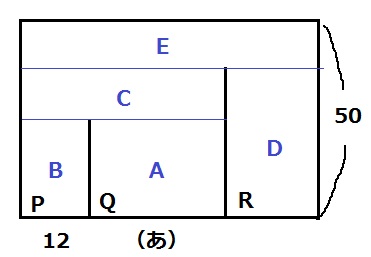
水が埋まる順番に、空間をA~Eに分ける。
AとBの体積比がわかれば、(あ)がわかる。
仕切りの高さがわからないので体積が何cm3か出せない。
そこで、何秒間で水が満たさせるか、グラフの時間の比から体積比を計算する。

グラフの読解は正確に!
図2はR(排水なし)、図3はP(排水あり)の水面変化。
図2はRだから、水面が上がるのはD~。
450秒後にE~となり、高さ50cmですべて水に満たされる。
図3はP。給水開始から3分30秒後に排水口を開き、その3分12秒後に排水口を閉じる。
つまり、給水から210秒~402秒に排水をしている。これ以外は排水していない。
折れ線の後ろから考えていくと、水面が50cmになる手前の上昇はE~。
402~537秒はP水面の高さが変化していない⇒D(Rのところ)
ということは、Dに水がはいる前に排水が行われている。
今度は0から考える。
0秒~150秒は0cm⇒A(Q)
150秒~210秒で急激に水面上昇⇒B(P)
折れ線の前後から検討して、排水が行われた210秒~402秒はCだと判明。
つまり、B→Cに流れたと同時に排水が始まり、C→Dに流れたと同時に排水が終わる。
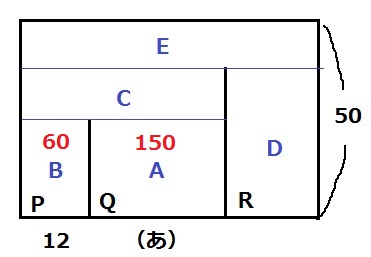
図3のグラフから、
Q(A):0~150秒⇒150秒間
P(B):150~210秒⇒60秒間
PとQの体積比は、P:Q=60:150=2:5
両者は仕切りの高さと奥行きが等しいので、横の長さは2:5
よって、(あ)=12×5/2=30cm
(2)
仕切りの高さとRの横の長さがわからないので、
A・B以外の体積比も水が満たされる時間で計測する。

図3で、210秒~402秒以外は排水の影響を受けない。
E:712-537=175秒
D:537-402=135秒
この時間は図2でも変わらないので、
図2のD~(A~Cが満たされる)は、450-135=315秒
満水は、450+175=625秒であることがわかる。

排水を行わない図2でA~Cの時間が315秒間かかったから、
残るCは、315-(150+60)=105秒間
体積比は、(A+B+C):D
=(150+60+105):135=7:3
Rの横は、42×3/7=18cm
横全体は、12+30+18=60cm
水槽全体の体積は60×40×50cm3で、排水なしで625秒で満たされる。
60×40×50÷625=毎秒192cm3
@別解@
A~D:Eの体積比から、仕切りイの高さがでる。
A~D:E=625:450=25:18
仕切りイの高さ=50cm×18/25=36cm
A~Cの体積は、42×40×36cm3となる。
一方で、図2(排水なし)と図3(排水あり)では満水時刻が、
712-625=87秒の差がある。
A~Cは315秒で満たされるので、
42×40×36÷315=192cm3
(3)
図3で排水を行った時間は、402-210=192秒間
排水を行わないとCは105秒、排水を行うとCは192秒で満たされる。
排水なしの給水速度は毎秒192cm3なので、
排水ありの給水速度は、192×105/192=毎秒105cm3
毎秒192cm3-毎秒105cm3=毎秒87cm3排水したことになる。



コメント