2019年度　淑徳与野中学過去問【算数】大問６解説

問題ＰＤＦ
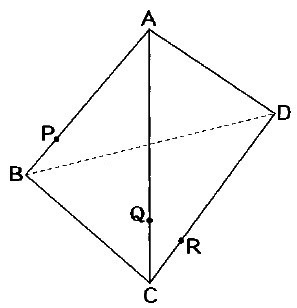
１辺の長さが８ｃｍの正三角形を４枚はり合わせて、下の図のような立体ＡＢＣＤを作りました。
点Ｐ、Ｑ、Ｒはそれぞれ辺ＡＢ、ＡＣ、ＤＣを３：１に分ける点です。
この立体を３点Ｐ、Ｑ、Ｒを通る平面で２つに切り分けます。
このとき、次の問いに答えなさい。

（１）
切り口の平面図形として最も適しているのものはどれですか。

（２）
切り口の平面図形のまわりの長さは何ｃｍですか。

（３）
切り分けた２つの立体の表面積の差は、正三角形ＡＢＣの面積の何倍ですか。

＠解説＠
（１）
断面図を作成。

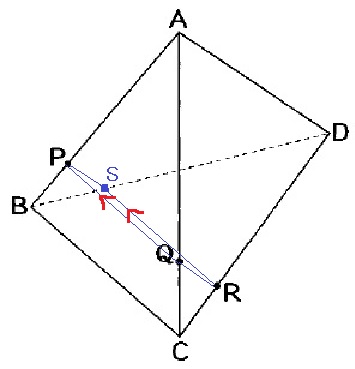
見にくいアングルだが…断面とＢＤの交点をＳとする。
ＰＱから切り込んでいくと、ＰＱとＳＲが平行になると感じられると思う。

正三角形は１辺の長さを確定すれば形が１つに決まるので、三角錐ＡＢＣＤは正三角錐。
△ＡＢＣと△ＤＢＣに注目！
２つの

正三角形は合同で、１辺を④とすると、ＰＱ＝ＳＲ＝③で等しい。

同様に、△ＢＡＤと△ＣＤＡでは、ＰＳ＝ＲＱ＝①で等しくなる。

つまり、断面の形は２組の対辺の長さが等しい→アの平行四辺形か、イの長方形。
△ＡＢＣを正面にとらえたとき、立体全体が左右対称の関係なので、イの長方形が答え。

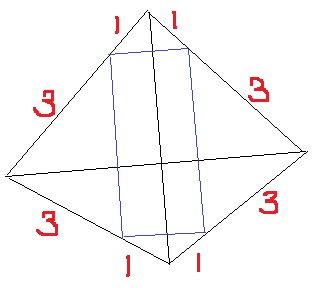
↑このアングルが長方形と認識しやすいかな？

（２）
先ほどの図で、④＝８ｃｍ
ＰＱ＝８×３/４＝６ｃｍ
ＰＳ＝８×１/４＝２ｃｍ
よって、長方形ＰＱＲＳの周りの長さは、（６＋２）×２＝16ｃｍ

（３）
大きい立体と小さい立体の表面積の差を求める。
断面ＰＱＲＳは等しいので相殺。差がでるのは正四角錘ＡＢＣＤの表面積にあたる部分。

１つの面の面積を④×④＝【16】として、断面を除いた小さい立体の表面積を求める。

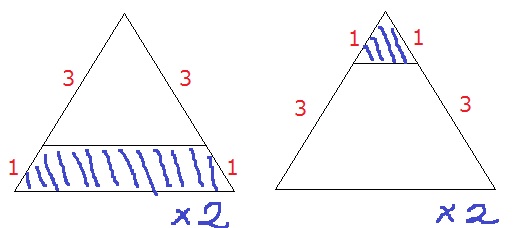
断面除く小…（【16】－【９】＋【１】）×２＝【16】

正四面体ＡＢＣＤの表面積は【16】×４＝【64】
断面除く大…【64】－【16】＝【48】

両者の表面積の差は【48】－【16】＝【32】
したがって、表面積の差は△ＡＢＣの面積の、【32】÷【16】＝２倍
難関中（算数科）解説ページに戻る