2022年度　早稲田中学２回目過去問【算数】大問２解説

問題ＰＤＦ
（１）
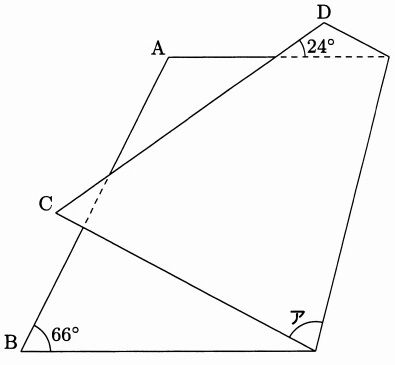
辺ＡＢと辺ＣＤの長さが等しい台形の紙を図のように折りました。
角アの大きさは何度ですか。

（２）
図の３つの点線ＰＡとＰＢとＰＣの長さの和は何ｃｍですか。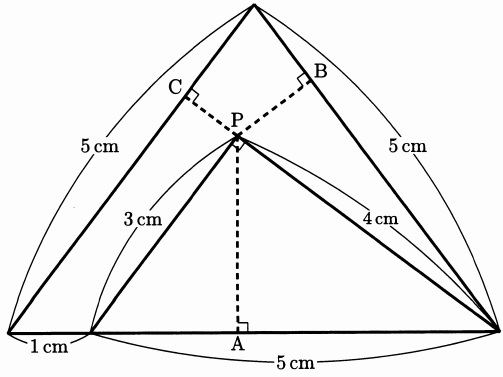

（３）
底面の半径が８ｃｍで高さが40ｃｍの円柱の容器と、
底面の半径が５ｃｍで高さが40ｃｍの円すいの形をしたおもりがあります。
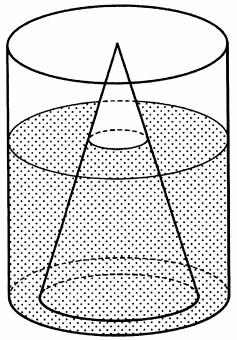
図のように、円柱の容器におもりを置いて、深さ24ｃｍまで水を入れました。
おもりを取り出すと水の深さは何ｃｍになりますか

＠解説＠
（１）

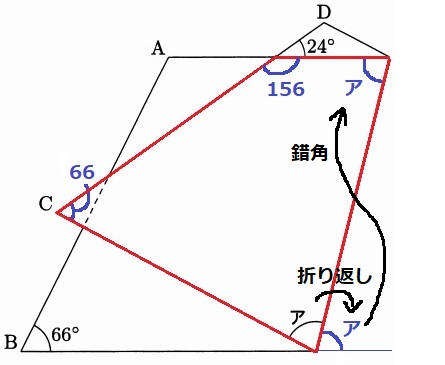
ＡＢ＝ＣＤである台形→四角形ＡＢＣＤは等脚台形（跳び箱）。
∠Ｃ＝66°

赤線の四角形に注目する。
180－24＝156°
折り返しと錯角で、内角の２つが∠ア。
ア＝（360－66－156）÷２＝69°

（２）
ややトリッキーな形です(-_-;)

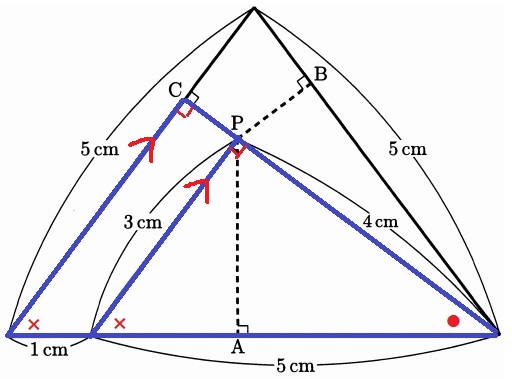
２つの直角から同位角が等しい⇒平行
２つの三角形は相似で、相似比は３：４：５。
内角が●—×—90°であれば、相似比は３：４：５である。

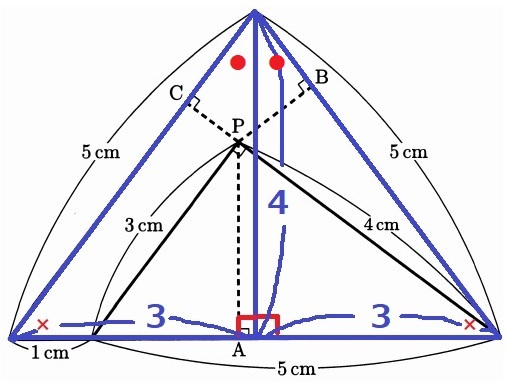
全体は等辺５ｃｍの二等辺三角形。
底角が×だから真っ二つに割ると、内角が●―×―90°の直角三角形があらわれる。
斜辺が５ｃｍなので底辺は６ｃｍ、高さは４ｃｍ。
二等辺の面積は、６×４÷２＝12ｃｍ²

では、どうやってＰＡ＋ＰＢ＋ＰＣを求めるべきか。。
こういうのは個別の長さがわからなくても和は求まる問題なので、
ＰＡ＋ＰＢ＋ＰＣを何かに置き換えられないか、という発想に持っていく。

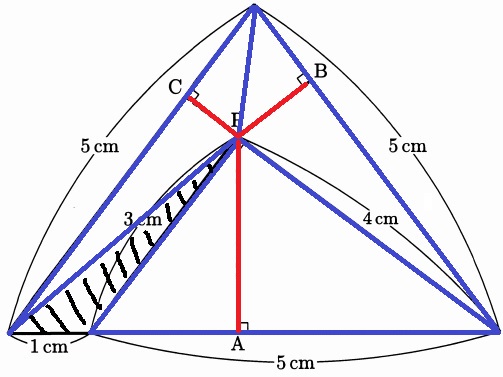
青線に囲まれた３つの三角形（斜線部分以外）に注目する。
いずれも底辺が５ｃｍで、高さの合計はＰＡ＋ＰＢ＋ＰＣにあたる。
３つの三角形の面積の和がわかれば、（面積）×２÷（底辺５）＝（高さの合計）
斜線部分の三角形が邪魔である。

●—×—90°の相似を直角三角形のなかにつくる。
△ＰＡＥの内角より相似比は３：４：５→ＰＡ＝３×④/⑤＝12/５ｃｍ
△ＰＤＥの面積は、１×12/５÷２＝６/５ｃｍ²

３つの三角形の和が、12－６/５＝54/５ｃｍ²
ＰＡ＋ＰＢ＋ＰＣ＝54/５×２÷５＝108/25ｃｍ

（３）

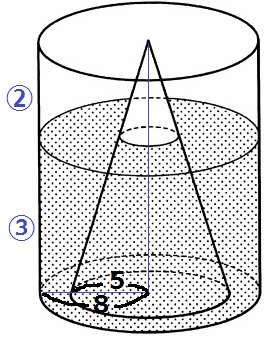
水の体積は、底面が半径８ｃｍ、高さ24ｃｍの円柱から、
半径５ｃｍ、高さ40ｃｍの円錐の下24ｃｍにあたる円錐台を引いたもの。

体積比なので、高さは16：24＝②：③で計算する。
円柱…８×８×3.14×③＝192×3.14
円錐台…円錐の体積比を５×５×５＝【125】とすると、上の小さい円錐は２×２×２＝【８】
円錐台の体積比は、【125】－【８】＝【117】
５×５×3.14×⑤÷３×【117】/【125】＝39×3.14

円柱の体積比は〔192〕、円錐台は〔39〕、水の体積は差の〔153〕。
おもりを出す前：出した後＝192：153＝64：51
底面積は半径８ｃｍの円で等しいので、高さの比は体積比にあたる。
24×51/64＝153/８ｃｍ
難関中（算数科）解説ページに戻る