問題PDF
(4)
ゆうじ君はお菓子屋さんに行きました。
このお店ではプリンをケーキよりも3割安く売っています。
1000円でプリンを5個買おうとすると、1000円でケーキを3個買ったときのお釣りの半分だけ
お金が足りなくなります。ケーキの値段は〔 〕円です。
(5)
ある鉄道は、上り電車と下り電車どちらも時速45kmで一定の間隔で運行しています。
太郎君はこの鉄道の線路に沿った道を、自転車で時速15kmの速さで走ると、
12分ごとに上り電車とすれ違いました。
このとき、太郎君は〔 〕分ごとに下り電車に追い抜かれます。
(6)
A君とB君とC君の3人の所持金の比は最初9:8:5でした。
3人がそれぞれ買い物をしたところ、A君とC君の残った所持金の差は3000円、
B君とC君の残った所持金の差は1800円になりました。
3人が使った金額の比が7:8:5だったので、A君の最初の所持金は〔 〕円です。
(7)
下の表は、16人の生徒が30点満点のテストを受けた結果を表したもので、
中央値が23.5点、平均値が24点でした。
このとき、表のアの人数は〔 〕人、エの人数は〔 〕人です。

(8)
あるクラスでテストをしたところ、クラス全体の平均点は58.5点で、
最高点と最低点の差は56点でした。
さらに最高点をとった1人を除いて平均点を計算すると57.4点、
最低点をとった1人を除いて平均点を計算すると59点になりました。
このとき、クラスの人数は〔 〕人で、最高点は〔 〕です。
(9)
A地からB地とC地を経由してD地まで行くのに、下の表のような行き方があります。
かかる時間の合計は1時間以内、運賃の合計は1000円以内となるような行き方は
〔 〕通りあります。ただし、待ち時間は考えないことにします。

(10)
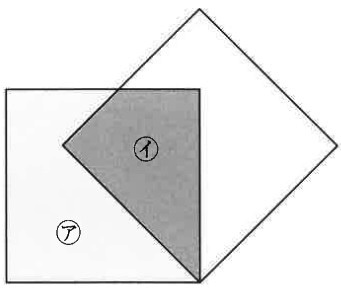
図は2つの合同な正方形が重なったものです。
アの図形とイの図形の面積の比が4:3のとき、
アの図形の周の長さとイの図形の周の長さの比は〔 〕:〔 〕です。
(11)
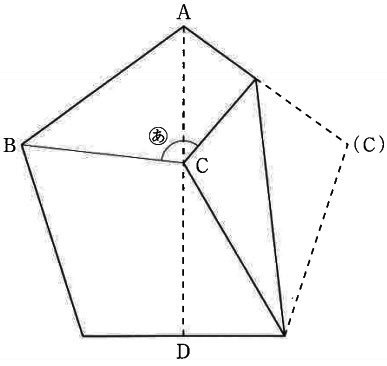
正五角形の形をした折り紙があります。
図のように、点Bと点Cが重なるように折り目ADをつけて戻した後、
点Cが折り目AD上にくるように折りました。
(あ)の角度は〔 〕度です。
(12)
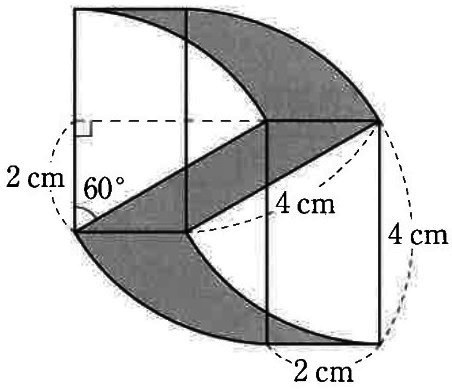
図はたて4cm、横2cmの2つの合同な長方形と
半径が4cm、中心角が60°の4つの合同なおうぎ形を組み合わせたものです。
色のついた部分の面積は〔 〕cm2です。
(13)
ある公園の噴水は、水のふき出しが図のように、2つの円に沿ってそれぞれ10個並んでいます。
噴水は決まった時刻になると、①のふき出しから水が出ます。
その後は1秒ごとに②→③→…→⑨→⑩の順で水がふき出し、
⑩までくると、今度は⑨→⑧→…→②→①の順で水がふき出します。
この動きを10分間くり返します。
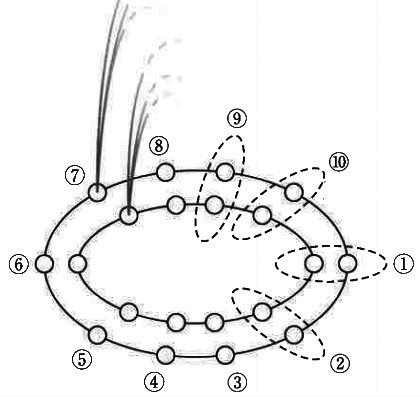
①噴水が始まってから2分後に水が出るのは〔 〕番のふき出し口です。
②ある日、外側の円の噴水の⑩のふき出し口が故障してしまいました。
そこで、内側の円の噴水はこれまで通りの動きで、外側の円の噴水は
①→②→…⑧→⑨→⑧→…→②→①の順で水がふき出すようにしました。
噴水が始まってから10分間で、内側と外側のどちらも①のふき出し口から
同時に水が出るのは〔 〕回です。ただし、噴水が始まったときを1回目とします。
(14)
直方体の形をした中央に仕切りがある水そうがあります。
この仕切りは左右に動かすことができ、
水そうの左側と右側には20cmの高さまで水が入っています。
①図1のように、水そうの左側に底面積が300cm2の直方体の形をしたおもりを
底まで入れたところ、水面の高さは〔 〕cmになりました。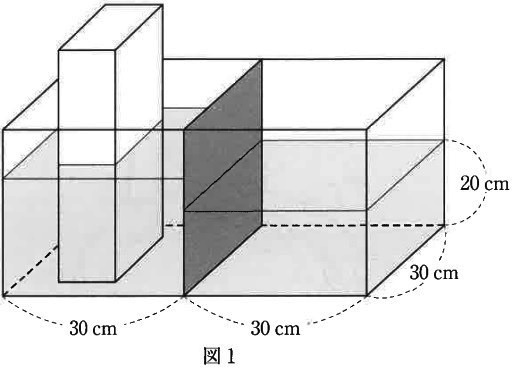
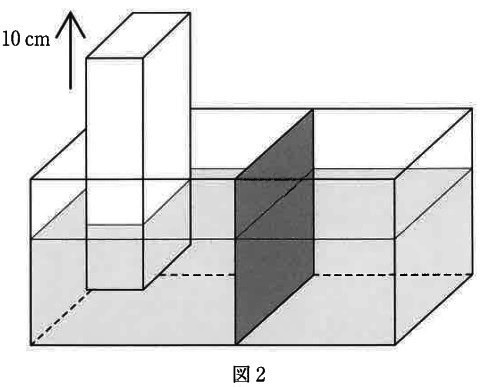
②図2のように、水そうの仕切りを右側に動かし、水そうの左側に入っていたおもりを
まっすぐ10cm持ち上げると水そうの左側と右側の水面の高さが同じになりました。
このとき、仕切りは右側に〔 〕cm動かしていて、水面の高さは〔 〕cmです。
@解説@
(4)
ケーキの値段を⑩、プリンの値段を⑦とする。
『1000円でケーキを3個買ったときのおつりの半分』
(1000-⑩×3)÷2=500-⑮円
1000円でプリン5個買うと、500-⑮円足りなくなるから、
⑦×5=1000+(500-⑮)
㊿=1500
ケーキの値段⑩は、1500×⑩/㊿=300円
(5)

太郎が電車とすれ違い、次の電車とすれ違うまで12分かかる。
このとき、両者は速さの和である時速60kmで近づく。
太郎が電車に抜かれるとき、『電車は一定間隔で運行している』ので、
太郎と次の電車の距離は先ほどと同じ。
→距離が同じなので、時間の比は速さの逆比。
両者は速さの差の時速30kmで近づく。
速さの比は、60:30=2:1
時間は逆比で1:2。12分×2=24分
(6)
BとCの最初の所持金は8:5で、使った金額の比も8:5である。
最初の所持金の比を〇、使った金額の比を△とする。
B-C
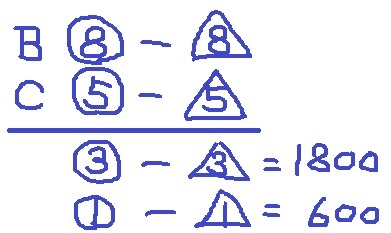
①-△1=600

⑦-△7をはさむ。
(⑦ー△7)と(⑤-△5)の差(②ー△2)=600×2=1200円
(⑨-△7)と(⑦-△7)の差は、3000-1200=1800円
この1800円は⑨と⑦の差の②にあたる。
したがって、Aの最初の所持金⑨は、1800×⑨/②=8100円
(7)
学習指導要領の改訂により、小6にデータの活用が組み込まれたことで、
中学受験界で扱うべきテーマがまた増えました・・(´゚д゚`)

中央値とは、値を大きい順(もしくは小さい順)に並べたときの真ん中の値。
16人の中央値は8番目と9番目の値の平均値である。
中央値が23.5点ということは8番目が23点、9番目が24点。
1~8番目が23点以下なので、ア=8-(1+2+1)=4人
平均点から16人の合計は、24×16=384点
イウエの合計点は、384-(20×1+21×2+22×1+23×4+26×5)
=384-306=78点
9番目以降の8人が24点以上のグループなので、イウエの人数の合計は8-5=3人
78を3人で均すと26点だから、3人で和が78点となる組み合わせは、
27点が2人で24点が1人。(26を基準とすると、27は1個上、24は2個下)
ア=4人、エ=2人
@別解@
平均点の24点を基準点とする。
負の数を使います。平均未満のグループにおいて、
23は24の1個下(-1)、22は2個下(-2)、21は3個下(-3)、20は4個下(-4)。
-1×4+(-2)×1+(-3)×2+(-4)+1=-16点
(わかりやすいように負の数を用いたが、平均より〇個下と考えて対処すればいい)
平均より上のグループで+16点にしなければならない。
26点の5人は、+2×5=+10
残り3人で+6点を稼ぐ。
0×1+(+3)×2、つまり、24点が1人、27点が2人。
@代表値@
公立高校入試ではいたるところで出てきます。
範囲(レンジ)…最大値-最小値
平均値…説明略
最頻値(モード)…最もあらわれている値。本問でいえば5人いる26点。
中央値(メジアン)…真ん中の順位の値。値の数が奇数か偶数かで処理が異なる。
11人の中央値は、(11+1)÷2=6番目の値
12人の中央値は、6番目と7番目の平均値となる。
(8)
本校では頻出問題。
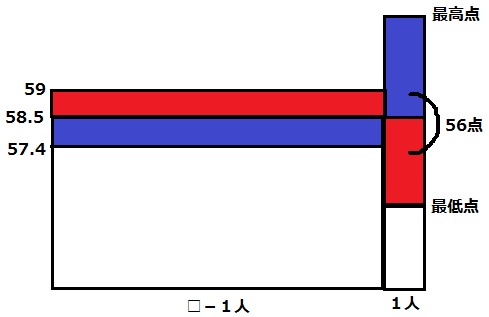
全体を□人とする。
最高点と最低点の1人を右に寄せ、残りの□-1人を左においた面積図で記す。
最高点者の1人を抜くと、最高点者の58.5より上の青い部分は左下の青い部分と同じで、
□-1人の平均が57.4点に下がる。
同様に、最低点者の58.5点より下の赤い部分が左上の赤い部分に相当する。
青と赤の長方形の面積の和は、最高点と最低点の差である56点。
左の青と赤の長方形に注目。
縦は59-57.4=1.6点
□-1=56÷1.6=35人
□=36人
最高点はクラス平均に青の長方形の面積を足せばいい。
58.5+35×(58.5-57.4)=97点
クラス人数…36人、最高点…97点
(9)
調査系なので後回し推奨。
◆Aでモノレールを選択→残り500円、45分
Bで高速船に乗ると残り0円と35分だから、Cは無料自転車。
Bで普通船に乗ると残り250円と25分だから、Cはバス。
◆Aで電車を選択→残り650円、40分
Bで高速船に乗ると残り150円と30分だから、Cはバスと無料自転車。
Bで普通線に乗ると残り400円と20分だから、Cは路面電車とバス。
◆Aでバスを選択→残り750円、30分
Bで高速船に乗ると残り250円と20分だから、Cはバス。
Bで普通船に乗ると残り500円と10分だから、Cはタクシーと路面電車。
以上、9通り。
(10)
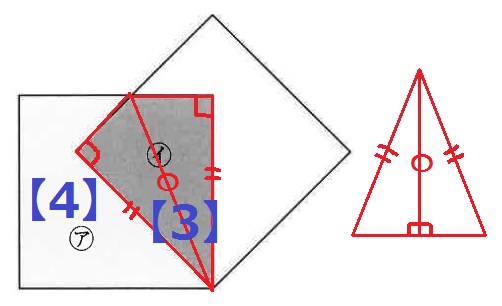
重なった部分に補助線をひく。
直角と共通辺、正方形の1辺が等しいことから、2つの三角形は合同。
(二等辺三角形を2つに割ったときの半分ずつは線対称で合同)
面積比の合計は【7】
知りたいのは周りの長さなので、正方形の1辺の長さを整数にすべく、
正方形の面積比は、【7】×7=【49】(平方数)で計算する。
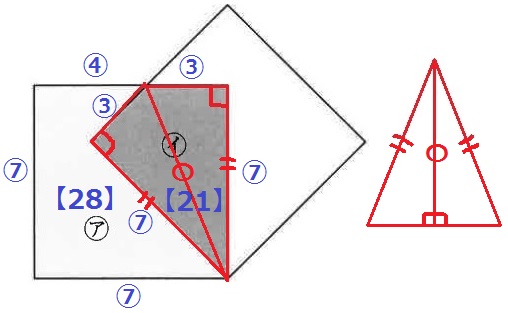
【49】=⑦×⑦→正方形の1辺の長さは⑦
重なり部分の三角形の面積比は【21】/2で長い辺の長さは⑦。
短い辺の長さは、【21】/2×2÷⑦=③
合同部分の長さは等しいので、アの周りの長さは正方形の周の長さである。
ア=⑦×4=㉘
イ=⑩×2=⑳
ア:イ=㉘:⑳=7:5
(11)
正五角形の内角の1つは108°
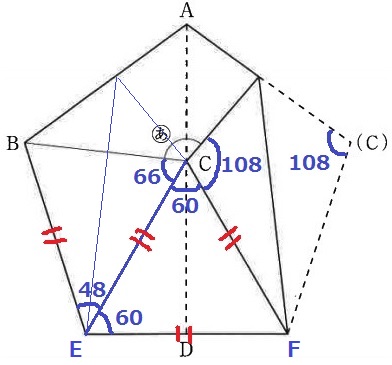
反対側も同じように折り返してみる。
△CEFの3辺はいずれも正五角形の1辺で長さが等しく、正三角形となる。
△BCEは二等辺三角形→∠BCE=(180-48)÷2=66°
(あ)=360-(66+60+108)=126°
(12)
中学受験ではお馴染みである。

赤い斜線の部分は、長方形と扇形を合わせた図形から扇形を引いた部分、
すなわち、長方形の面積に相当する。

下は扇形の先と正方形で同様のことをすると、斜線部分は正方形になる。
左に全て寄せると長方形となり、2×6=12cm2
(13)①
周期算。区切りの良いところを1グループとおく。
留意点は『噴水は決まった時刻になると①のふき出し口から水が出る』ので、
噴水が始まってから1秒後は、①ではなく②のふき出し口から水が出る。
【②→③→…→⑨→⑩→⑨→…→②→①】の18個を1グループとする。
120秒÷18=6…12
余り12は⑦
②
内側は先ほどと同じ、1グループ18個。
外側は【②→③→…→⑧→⑨→⑧→…→②→①】で1グループ16個。
18と16の最小公倍数は144。
つまり、144秒ごとに内側と外側の①が同時に吹き出す。
600秒÷144=4…24
留意点は『噴水が始まったときを1回目とする』ので、1秒後の②の前の①もカウントする。
したがって、5回。
(14)①

最初は中央に仕切りがあるので、左右の水の体積は同じ。
右の底面積は、30×30=900cm2
左の底面積は、900-300=600cm2
底面積の比は、右:左=900:600=3:2
体積が等しいので、高さの比は底面積の比の逆比で2:3
20×3/2=30cm
②
水面が左右同じ→仕切りを外してもよい。
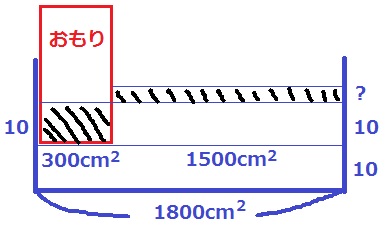
おもりが押しのけている水の体積と、それにより上昇した部分の水の体積は同じ(斜線部分)
底面積の比は、300:1500=1:5
高さの比は逆比だから、?=10cm×1/5=2cm
よって、水面の高さは22cm。
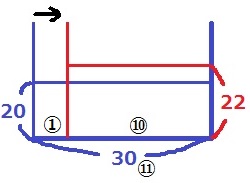
仕切りの右側部分だけを考える。
最初は20cmだった、仕切りを右に移動すると22cmになった。
高さの比は、20:22=10:11
底面積の比は逆比で11:10
奥行きは30cmで共通だから、面積比は横の長さの比に依存する。
移動前の横の長さ30cmを⑪とおくと、移動後の横の長さは⑩、仕切りを移動させた長さは①となる。
仕切りを動かした長さは、30×①/⑪=30/11cm
仕切りの移動距離…30/11cm、水面の高さ…22cm



コメント