問題ＰＤＦ
図のような円周の形をした歩道があります。
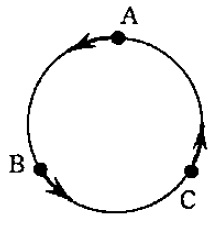
この歩道を３等分する地点からＡ、Ｂ、Ｃの３人が同時に出発しました。
矢印の方向に、それぞれ一定の速さで歩き始めたところ、
出発してから６分後にＡが初めてＢに追いつき、
出発してから20分後にＡが初めてＣに追いつきました。
（１）
Ｃが初めてＢに追いつくのは、出発してから何分後ですか。
（２）
Ｃが初めてＢに追いついたとき、Ａはこの歩道をちょうど10周して出発地点に来ていました。
Ｂ、Ｃがこの歩道を１周するのにかかる時間はそれぞれ何分何分後ですか。
＠解説＠
（１）
時間の情報しかないので、最初に適当な距離を決めてしまう。
６と20の最小公倍数である60ｍを１周の長さとする。
旅人算。
ＡはＢの後方20ｍから追いかける。
20ｍ÷（Ａの速さ－Ｂの速さ）＝６分
Ａの速さ－Ｂの速さ＝分速10/３ｍ
ＡはＣの後方40ｍから追いかける。
40ｍ÷（Ａの速さ－Ｃの速さ）＝20分
Ａの速さ－Ｃの速さ＝分速２ｍ
速さはＣ＞Ｂ
ＣとＢの速さの差は、10/３－２＝分速４/３ｍ
ＣはＢの後方40ｍから追いかけるので、
40ｍ÷分速４/３ｍ＝30分後
（２）
前問より、ＣがＢに追いつくのは30分後。
その間にＡは10周するので、Ａは１周を３分で歩く。
Ａは６分後にＢに追いつくので、Ａはちょうど２周歩く。
Ｂは２－１/３＝５/３周歩く。
距離の比は速さの比。
Ａ：Ｂ＝２：５/３＝６：５
時間の比は速さの逆比。
Ａ：Ｂ＝５：６
Ａが１周３分だから、Ｂは３×６/５＝18/５＝３分36秒
Ｃも同様。
ＡがＣに追いつく20分後に、Ａは20÷３＝20/３周歩く。
Ｃは、20/３－２/３＝６周歩く。
速さの比は、Ａ：Ｃ＝20/３：６＝10：９
よって、３×10/９＝10/３＝３分20秒
難関中（算数科）解説ページに戻る
コメント