2019年度　大阪星光学院中学過去問【算数】大問５解説

問題ＰＤＦ
下の図１のような水の入っていない直方体の水そうの中に、底面に垂直で側面に平行な高さが20ｃｍと60ｃｍの仕切りがあります。仕切りの厚さは考えません。仕切りで区切られたところを左からＡ、Ｂ、Ｃとします。

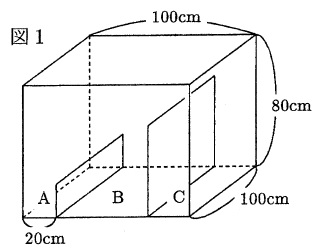
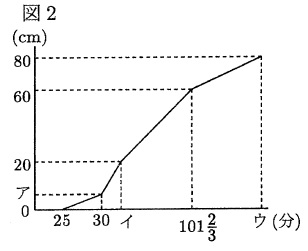
Ａのそこには毎分一定の量で水が出ていく栓があり、はじめは開いています。Ａには毎分２ℓ、Ｃには毎分一定の量で水を入れる蛇口がついていて、同時に水を入れ始め、10分後に栓を閉じます。水を入れ始めてから25分後に、ＡからＢに水が移り始めました。下の図２のグラフは水を入れ始めてからの時間とＢの水面の高さの関係を表しています。

（１）
栓から出ていく水の量は毎分〔　　　〕ℓです。

（２）
101・２/３分までに両方の蛇口から出た水の量は合わせて〔　　　〕ℓであり、
Ｃの蛇口から出る水の量は毎分〔　　　〕ℓです。

（３）
図２のア＝〔　　　〕、イ＝〔　　　〕、ウ＝〔　　　〕です。

（１）
はじめはＡだけを考える（蛇口Ｃは無視）。
Ａの蛇口を開いてから10分後に栓を閉じ、その15分後にＡからＢに水が漏れる。

Ａの容積（高さ20ｃｍ）をだす。
100×20×20＝40000ｃｍ³＝40ℓ
Ａの蛇口は毎分２ℓの水がでるので、
40ℓ÷２ℓ＝20分でＡが満たされるはず。
余分に５分かかったのは、10分間Ａの栓が開いていたから。
Ａの蛇口５分間で、２ℓ×５分＝10ℓの水が溜まる。
これが栓から出て行った水の量に匹敵する。
栓が開いていたのは10分間なので、
栓から出て行く水の量は毎分、10ℓ÷10分＝１ℓとなる。

（２）

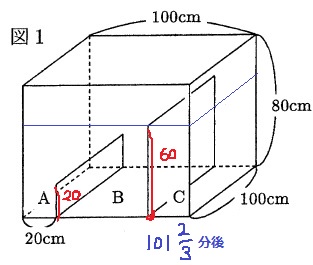
101・２/３分は60ｃｍまで満たされる。
その容積は、100×100×60＝600000ｃｍ³＝600ℓ
蛇口Ａのは10分間、栓から水が出ている。
その量は前問より、１ℓ×10分＝10ℓ
よって、蛇口Ａ＋蛇口Ｃの合計は、600ℓ＋10ℓ＝610ℓ

610ℓ÷101・２/３分間＝毎分６ℓずつ水を入れている。
蛇口Ａは毎分２ℓだから、蛇口Ｃは、毎分６ℓ－毎分２ℓ＝毎分４ℓ

（３）
グラフの意味をつかむ。

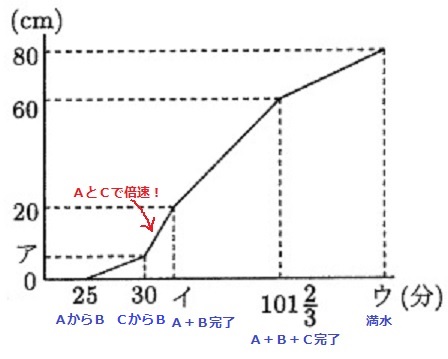
アの30分後は、ＣからＢに水が漏れてくるとき。
前問より、蛇口Ｃは毎分４ℓの水がでてくるので、
30分間では、４×30＝120ℓ＝120000ｃｍ³

これがＣの部分に容積に相当する。
ここからＣの横幅が出せる。
120000ｃｍ³÷100ｃｍ÷60ｃｍ＝20ｃｍ
Ｂの横幅は、100－20－20＝60ｃｍ

25～30分後の５分間でＢへの入水は蛇口Ａ（毎分2000ｃｍ³）のみなので、
2000ｃｍ³×５分÷100ｃｍ÷60ｃｍ＝５/３ｃｍ・・ア

30分後、Ｂの場所で高さ20ｃｍまで残りは、
20ｃｍ－５/３ｃｍ＝55/３ｃｍ
蛇口Ａと蛇口Ｃ（毎分6000ｃｍ³）で入水。
60ｃｍ×100ｃｍ×55/３ｃｍ÷6000ｃｍ³＝55/３分
30＋55/３＝145/ 3 分・・イ

高さ60～80ｃｍの20ｃｍ分の容積を求める。
100×100×20＝200000ｃｍ³＝200ℓ
蛇口ＡとＣ（毎分６ℓ）で入水。
200ℓ÷６ℓ＝100/３分
101・２/３分＋100/３分＝135分・・ウ
難関中（算数科）解説ページに戻る