問題PDF
1辺の長さが1cmの立方体をすき間なく積み重ねて直方体を作り、
図のように2点A、Bをとります。
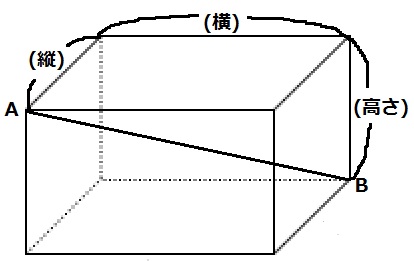
このとき、次の問いに答えなさい。
(1)
(縦)×(横)×(高さ)が次のようの直方体について、
直線ABはいくつの立方体の中を通りますか。
(ア)(2cm)×(5cm)×(3cm)
(イ)(2cm)×(6cm)×(3cm)
(ウ)(12cm)×(20cm)×(30cm)
(2)
(縦)×(横)×(高さ)が(30cm)×(42cm)×(□cm)の直方体について、
直線ABは66個の立方体の中を通ります。□にあてはまる数は全部で何通りありますか。
@解説@
(1)(ア)
串刺しの基本は縦の辺と横の辺に区切って考える。
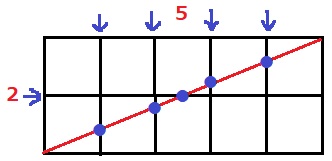
最初は縦と横の平面で考える。
直線が辺と交わるたびに正方形を突き刺す。
縦の辺は2-1=1つ、横の辺は5-1=4つ
●は5つあるので5回突き刺す。
1回目の突き刺しの前に最初の正方形を突き刺しているから、
直線が通過する正方形は5+1=6個
まとめると…【(縦の辺-1)+(横の辺-1)+1】
これは3次元の立体でも同様のことがいえる。
【(縦の辺-1)+(横の辺-1)+(高さの辺-1)+1】
答えは、(2-1)+(5-1)+(3-1)+1=8個
(イ)
前問の2・3・5は1以外に共通の約数を持たなかった(互いに素)
しかし、2・3・6ではうまくいかない。
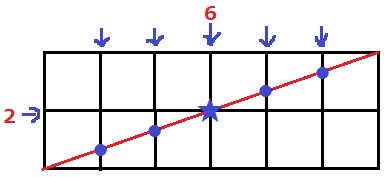
2×6の平面でやってみると直線が格子点(★)を通過する。
先ほどの公式を適用すると、(2-1)+(6-1)+1=7個となるが、
実際に直線が通過する正方形の数は6個。
それは格子点を通るたびに突き刺される正方形の数が減るからである。
格子点★は(縦)2等分の1つ目、(横)6等分の3つ目にあらわれる。
→1/2=3/6→通分時に分母が最大公約数となるのと同じ!
この最大公約数に注目すると、格子点の個数は〔最大公約数-1〕個で7-1=6個となる。
空間の場合は縦・横・高さと3つの数字がでてくるから、
(縦・横)(横・高さ)(高さ・縦)の最大公約数をいちいち出さねばならない…。
さらに(縦・横・高さ)の最大公約数分、格子点を重複して引いたので、
最後に3つの最大公約数を足して帳尻を合わせなくてはならない。
2×6×3の直方体では、
2・6の最大公約数→2…格子点は2-1=1個
3・6の最大公約数→3…格子点は3-1=2個
2・3の最大公約数→1…格子点は1-1=0個
2と3と6の最大公約数→1…格子点は1-1=0個
(2-1)+(6-1)+(3-1)-(1+2+0)+0+1=6個
*再度かくと、最後の+1は前問に登場した式の最後の+1です。
@別解@
原理の説明は先の通りだが、-1の数を減らすことができる。
■平面■
2×6の平面の場合。
(2-1)+(6-1)-(2と6の最大公約数-1)+1
=(2+6)-(2と6の最大公約数)
*前半の-2と後半の+2が相殺できる。
■空間■
2×6×3の空間の場合。
(2-1)+(6-1)+(3-1)-(2と3の最大公約数-1)-(2と6の最大公約数-1)-(3と6の最大公約数-1)+(2と3と6の最大公約数-1)+1
=(2+3+6)-(2と3の最大公約数+2と6の最大公約数+3と6の最大公約数)+(2と3と6の最大公約数)
*-3と+3、-1と+1で相殺できる。
まとめると、
【公式】
a×bの平面…(a+b)-(aとbの最大公約数)
a×b×cの空間…(a+b+c)-(a・bの最大公約数+b・cの最大公約数+c・aの最大公約数)+(a・b・cの最大公約数)
*スッキリして使いやすいが、原理を理解したうえで公式を使いたい。
(ウ)
公式を適用。
12と20の最大公約数→4
20と30の最大公約数→10
12と30の最大公約数→6
12と20と30の最大公約数→2
(12+20+30)-(4+10+6)+2=44個
(2)
試しに長さがわかっている30cmと42cmの平面で調べると、
(30+42)-6=66個
ということは、新しく串刺しされる立方体を1つも出さない高さが答え。
ところで、先ほどの公式を観察すると、整数の問題にでてくるアレと似ている|д゚)
『100までの整数のうち、2の倍数と3の倍数と5の倍数は何個あるか?』

ベン図。
2の倍数と3の倍数と5の倍数の個数を足し、2つの最小公倍数となる3ヶ所を引き、
最後に3つの最小公倍数を足して求める。処理過程が一緒!

新しく突き刺さる立方体がないので、□の円では上の部分がゼロになる。
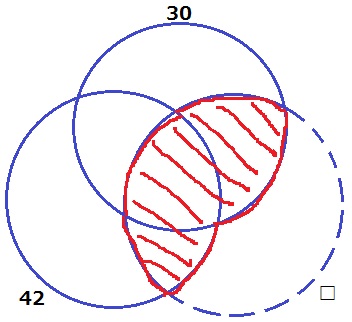
つまり、□の部分は赤い斜線の面積。
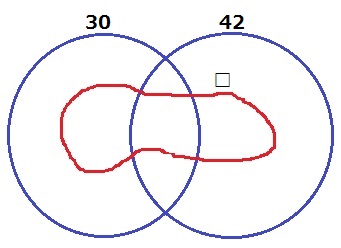
もっと変形させると、□は30と42の集合に包含している。
□の要素を確認する。
直線ABを30等分もしくは42等分したとき、
□等分の目盛りが30等分もしくは42等分の目盛りとすべて重なれば、
新たな目盛りができない=通過する立方体は66個のままになる。
言い換えれば、30を□で割って割り切れる数、または42を□で割って割り切れる数。
30と42の約数に注目する。
30の約数→1・2・3・5・6・10・15・30
42の約数→1・2・3・6・7・14・21・42
重複を除くと、高さは〔1・2・3・5・6・7・10・14・15・21・30・42〕cm
したがって、12通りとなる。



コメント