問題ＰＤＦ
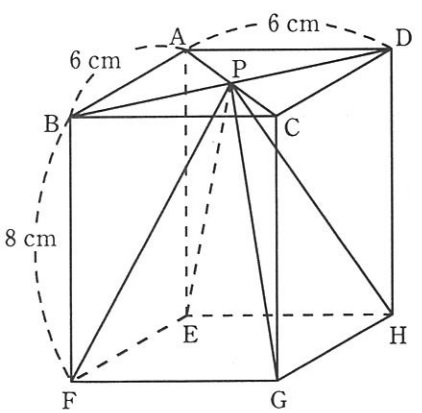
下の図のような直方体ＡＢＣＤ―ＥＦＧＨがあり、ＡＢ＝ＡＤ＝６ｃｍ、ＢＦ＝８ｃｍです。
正方形ＡＢＣＤの２本の対角線ＡＣ、ＢＤの交点をＰとします。
４点Ａ、Ｆ、Ｇ、Ｄを通る平面と四角すいＰ―ＥＦＧＨの辺ＰＥ、ＰＨとの交点を
それぞれＱ、Ｒとします。
（１）
長さの比ＰＲ：ＲＨを最も簡単な整数の比で表しなさい。
（２）
四角形ＱＦＧＲの面積は四角形ＡＦＧＤの面積の何倍ですか。
（３）
四角すいＰ―ＥＦＧＨを４点Ａ、Ｆ、Ｇ、Ｄを通る平面で２つに切り分けるとき、
点Ｅをふくむ方の立体の体積を求めなさい。
ただし、角すいの体積は（底面積）×（高さ）÷３で求められます。
＠解説＠
（１）
台形ＱＦＧＲは長方形ＡＦＧＤ上にある。
右から眺めると、ＲＧとＤＧがかぶる。
正方形ＣＧＨＤに転写すると右図のようになる。
△ＰＤＲと△ＨＧＲは相似で、相似比はＰＲ：ＲＨ＝１：２
（２）
台形ＱＦＧＲと長方形ＡＦＧＤを一緒に観察できる方向⇒正方形ＡＢＣＤに転写する。
（前方の正方形ＢＦＧＣでも良い。上方向だと対角線ＡＣ、ＢＤがあるので様子がわかりやすい）
ＱはＡＣ上、ＲはＢＤ上にくる。
前問の１：２を活用。
△ＰＱＲを①とする。ＱＰ：ＰＣ＝１：３より、△ＰＲＣ＝③
ＲＰ：ＰＢ＝１：３より、△ＰＢＣ＝⑨
同様に、△ＢＱＰ＝③
台形ＱＢＣＲ（立体ではＱＦＧＲ）の面積は⑯。
正方形ＡＢＣＤ（立体ではＡＦＧＤ）は△ＰＢＣの４倍で㊱。
台形ＱＦＧＲは長方形ＡＦＧＤの16/36＝４/９倍
（３）
ＦＧ、ＥＨ、ＱＲの中点をそれぞれＳ、Ｔ、Ｕとして、
四角錐ＰーＥＦＧＨを△ＰＳＴで２等分する。
△ＰＳＴを底面として左右の最大幅を高さとみなす。
底面積の比は、青の立体：赤の立体＝△ＰＵＳ：△ＵＴＳ＝ＰＵ：ＵＴ＝①：②
高さは断頭三角柱の高さの平均を用いる。
Ｐ…０ｃｍ、ＦＧ…６ｃｍ、ＱＲ…△ＰＱＲと△ＰＥＨの相似で、ＱＲ＝６×１/３＝２ｃｍ
青の立体の高さは、（０＋２＋６）÷３＝８/３ｃｍ
赤の立体の高さは、（２＋６＋６）÷３＝14/３ｃｍ
高さの比は、青：赤＝８/３：14/３＝【４】：【７】
体積比は底面積の比×高さの比で、青：赤＝①×【４】：②×【７】＝２：７
四角錐ＰーＥＦＧＨの体積から体積比を用いて、
求積すべき赤の立体の体積は、６×６×８÷３×７/９＝224/３ｃｍ3
＠＠＠
宮崎の大問６で類題が出ています。
最後の（３）です。正答率は0.4％、中学生も苦戦してます。
（２）は根号がでてしまいますが、45°がどこにあたるかを図示できれば、
（３）は誘導無視で解くことができます。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント