2023年度　女子学院中学過去問【算数】大問５解説

問題ＰＤＦ
2023枚の折り紙をＪ、Ｇの２人で分けるのに、同じ枚数ずつＪ、Ｇ、Ｇ、Ｊ、Ｊ、Ｇ、Ｇ、Ｊ、Ｊ…の順に取っていき、最後にその枚数が取れなかった場合も順番通りの人が残りをすべて取ることにします。例えば、20枚ずつだとＪは1020枚、Ｇは1003枚で、30枚ずつだとＪは1003枚、Ｇは1020枚もらえます。

（１）
23枚ずつ取ると、Ｊは〔　　　〕枚もらえます。

（２）
〔　　　〕枚ずつだとＪは1023枚もらえます。ただし、答えは素数です。

（２）
Ｊは1023枚。
Ｇの枚数は、2023－1023＝1000枚

ＪとＧのどちらで終わったのかがわかれば、
最後の残りを受け取らなかった方の枚数の約数が一度に取る枚数である。

↑全部取ったら満額とする。
周期のはじめのＪが残りを取る場合を考える。
手前のＪＧＧＪまではＪとＧの回数が同じ＝枚数が等しい。
残りはＪが引き受けるのでＪの方が多い→ありえる。

Ｇはすべて満額で1000枚に達したので、一度に取る枚数は1000の約数である。
Ｊは最後の満額で1000枚に達し、残りが23枚になる。
ということは、一度に取る枚数は少なくとも23枚以上。
1000を素因数分解すると、1000＝２×２×２×５×５×５
最大の素数は５、23以上ではない。よって、×！

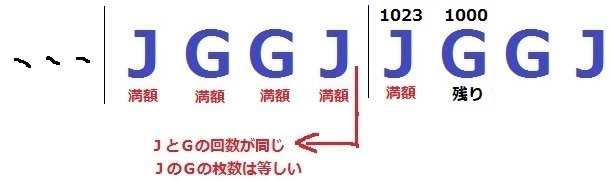
最初のＪが満額で、次のＧが残りを取る場合。
満額回数の多いＪの方が枚数が多い→ありえる。
Ｊはすべて満額なので、１回に配る枚数は1023の約数。
1023＝３×11×31
23以上の素数は31しかない。
31枚？

他も検討してみる。２個目のＧが残りを取る場合。
ＪＧまで枚数が等しい。
次のＧが残りを引き受けると、Ｇの方がＪより多くなる→ありえない×

最後のＪが残りを取る場合。
Ｇの満額回数がＪより多いのでありえない。×
したがって、31枚。
難関中（算数科）解説ページに戻る