問題PDF
(1)
2つの数を1より大きな数で割った余りを考えます。
(あ)83と135をある数で割ると、余りが同じになりました。
このようなある数と余りの組合わせを(割る数、余り)の形ですべて答えなさい。
(い)次の条件を満たすような〔 〕に入る最も小さい数を答えなさい。
「41と〔 〕をある数で割ると、余りが同じになりました。
このようなある数と余りの組合せは5組あります。」
(2)
リンゴがAの箱には219個、Bの箱には325個、Cの箱には410個入っています。Aの箱に入っているリンゴを一袋に入れる個数が同じになるように袋詰めしたところ、いくつかリンゴが残りました。B、Cの箱に入っているリンゴについてもAの箱の場合と同じ個数のリンゴを袋詰めしたところ、Bの箱には、Aの箱よりも1個多く、Cの箱にはBの箱よりも1個多くリンゴが残りました。そこで、この3つの箱に残ったリンゴを集めて同じように袋詰めをしたら、やはりいくつか残りましたが、その残りは作業をしてくれたみんなで分けました。
「あらかじめBの箱から1個、Cの箱から2個のリンゴを取り出しておけば、Aの箱のリンゴと同じ個数ずつ袋詰めしたときの余りは同じになる。」ことを使って(1袋に詰めたリンゴの個数、袋詰めに使った袋の枚数)の組合せをすべて答えなさい。
@解説@
(1)
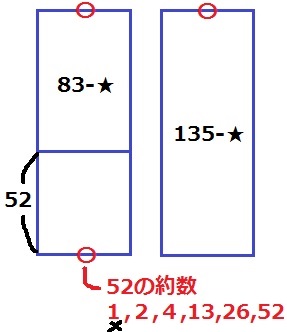
割る数を〇、余りを★とする。
余りの★を除外した(83-★)と(135-★)は〇で割り切れる。
差の(135-★)-(83-★)=135-83=52も〇で割り切れる。
つまり、〇は52の約数である。
問題文より「割る数は1より大きい数」なので、
〇=2、4、13、26、52
83÷2=41…1
83÷4=20…3
83÷13=6…5
83÷26=3…5
83÷52=1…31
(割る数、余り)=(2、1)(4、3)(13、5)(26、5)(52、31)
(い)
先ほどの逆の手順をおこなう。
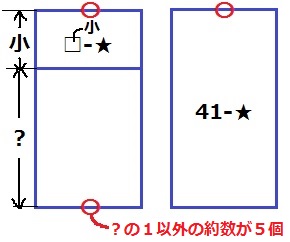
求める数を□とする。
(□-★)と(41-★)は〇で割り切れる。
2数の差は?で、〇は?の1以外の約数である。
『〇と★の組合せが5組』→?の約数は1を含めて6個。
□は最も小さい数なので、?を大きくとる必要がある。
41未満で約数が6個の最大数は32。?=32
(41-★)-(□-★)=32
41-□=32
□=9
(2)
前問の考えがヒントになっている。
おまけに、あらかじめB-1、C-2をしておけば余りが同じになるとダダ漏れ。。
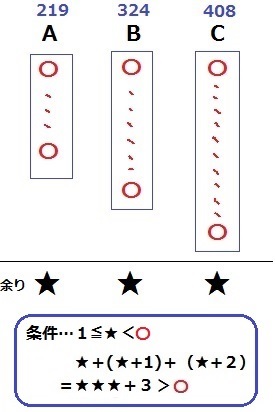
A=219個、B-1=324個、C-2=408個で1袋に〇個ずつ袋詰めをする。
すると、余りはすべて★になる。
それぞれの条件を確認しておく。
まず、Aの袋詰めで余りが発生したので★は1以上。
余りの★は割る数の〇より小さい⇒1≦★<〇
また、あらかじめ3個除外したので、実際の余りは★★★+3個。
これをさらに〇個ずつ袋詰めして余ったから、★★★+3>〇でなくてはならない。
条件をまとめると、1≦★<〇<★★★+3
(1)の考えを適用して、
(324-★)-(219-★)=324-219=105
(408-★)-(324-★)=408-324=84
105と84の最大公約数は21→21の約数は〔1、3、7、21〕
条件から〇は1より大きいので、〇=〔3、7、21〕
〇=3…Aの219は位の和が3の倍数だから余り★が0になってしまう…。
1≦★の条件を満たさない。×!
〇=7…219÷7=31…2
★★★+3=2×3+3=9>7 条件適合!
(219+325+410)÷7=954÷7=136…2
〇=21…219÷21=10…9
★★★+3=9×3+3=30>21 条件適合!
954÷21=45…9
(1袋当たりの個数、袋の枚数)=(7、136)(21、45)



コメント