問題PDF
(1)
図は正六角形1つと、正五角形2つを並べたものです。角アの大きさは何度ですか。
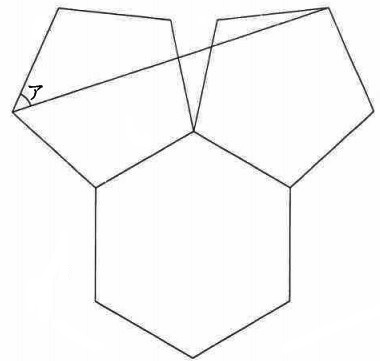
(2)
図の四角形ABCDの面積が63cm2のとき、五角形ABCEFの面積は何cm2ですか。
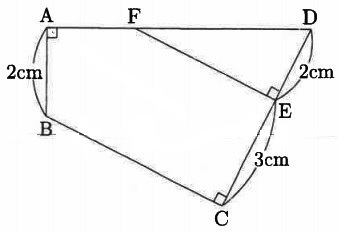
(3)
図のように、1辺の長さが6cmの正方形1つと、直角二等辺三角形4つ、
正三角形2つを並べると、ある立体の展開図になります。
この図を組み立ててできる立体の体積は何cm3ですか。 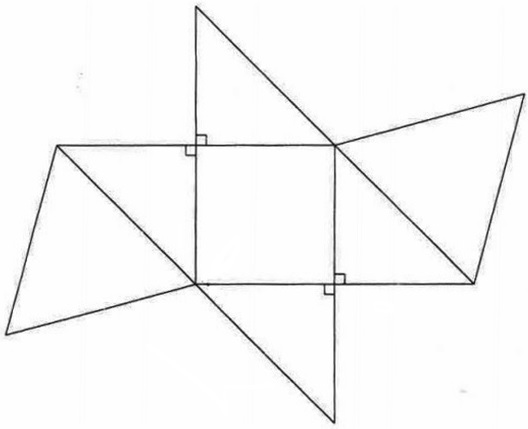
@解説@
(1)
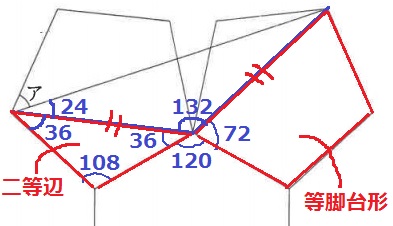
合同な正五角形の対角線で二等辺三角形をつくる。
左下は正五角形の1辺を等辺とする二等辺。
右は正五角形からその二等辺をのぞいた等脚台形。
360-(36+120+72)=132°
(180-132)÷2=24°
ア=108-(24+36)=48°
@余談@

いろいろ粘って試してみたのですが、これ以外の方法ってあるのでしょうか?
解法を知っているかどうかで決着つきそうな…。
∠アをなす線分が二等辺三角形の等辺ではなく、最も長い辺にしないとうまくいかないと思う。
初見殺しな気がするので経験しておこう。
■追記■
— Nick Kalapodis (@NickKalapodis) February 15, 2021
△KGMは正三角形になるそうです。
(2)

2cmの等辺があって、左側がブツ切りされているように見える。
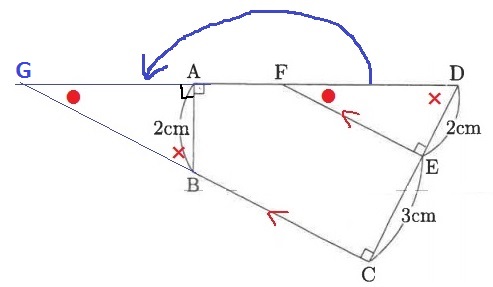
DAとCBを延長して、左側に△ABGをつくってみる。
∠DEF=∠DCG=90°より、FEとGCが平行。
●+×=90°で●を同位角で移動させると、△ABGの残りの角である∠ABG=×となり、
△ABGと△EDFは1辺と両端角が等しく合同。
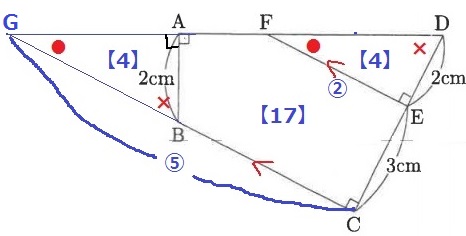
辺の比はDE:DC=2:5なので、面積比は△DEF:△DCG=【4】:【25】
五角形ABCEF=【25】-【4】×2=【17】
四角形ABCD=【21】だから、五角形ABCEFの面積は63×17/21=51cm2
(3)

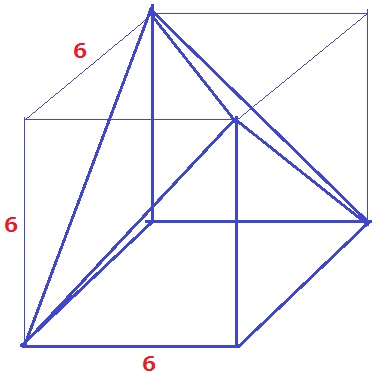
正方形を底面として直角をヒントにすると、4つの直角二等辺三角形は垂直に立つ。
1辺6cmの立方体から2つの三角錐をひいた立体になる。
6×6×6-6×6÷2×6÷3×2
=144cm3



コメント
(2)の最後の計算が「63×17/21=54cm2」となっていますが、51cm2の誤りではないでしょうか。
あ”あ”っ!
大事なところをミスしていました…。
訂正しました。ご指摘ありがとうございますm(_ _)m