問題ＰＤＦ
〔例〕のような４×４のマス目があり、それぞれのマス目に数字を入れていきます。
入れる数字は、１、２、３、４のいずれか１つですが、次のようなルールがあります。
①縦、横とも、同じ列には、すべて異なる数字が入ります。
②例のように、２×２マスに分けられている４つのブロックに入る数字もすべて異なります。
以下は、Ｘ君とＹ君の会話です。
Ｘ：こんな表をもらったんだけど、ルール通りに数字を入れるとすると、
何通りの数字の入れ方があるんだろう。
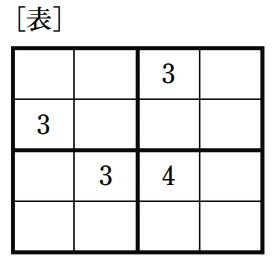
Ｙ：難しいね。どこか数字が決まるところはないのかな。
Ｘ：３が３か所に入っているから、あと１つどこかに入るはずだよね。
あっ、わかった。Ａのところに入る数字は３じゃない？
Ｙ：本当だ。どの列にも同じ数字は１個しか入れないから、Ａが３だよね。
Ｘ：ほかに、数字が決まるところはないかな？
Ｙ：うーん、ないみたいだね。だったら、いくつか数字を当てはめて考えてみようよ。
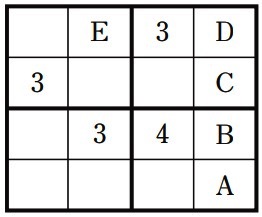
Ｘ：じゃあ、表のＣなんだけど、１、２、４のどれかが入るんだよね。
例えば２が入るとしてみたらどうなるかな。
Ｙ：そのときは、ＢとＤに入る数字が決まるよね。
Ｘ：あっ、だったらＥに入る数字も決まるよ。
（１） 483名中431名正解
Ｄ、Ｅに入る数字を答えなさい。
Ｙ：残ったマスもすべて数字が決まるよね。
Ｘ：本当だね。今度はＣが１のときを試してみようかな。
そうすると、表のＦに入る数字も決まるよ。
（２） 483名中385名正解
Ｆに入る数字を答えなさい。
Ｘ：へぇ、可能性のある数字を順番に当てはめていけば、きちんと数えることができるんだね。
あとはＣが４のときだけど、これはちょっと大変かな。
Ｙ：大丈夫だよ、ていねいにやれば数え上げられるさ。
Ｘ：そうだね。何とかできそうだ。
わかった、最初の表では、全部で ア 通りの数字の入れ方があるんだ！
（３） 483名中142名正解
ア に当てはまる数字を答えなさい。
＠解説＠
（１）
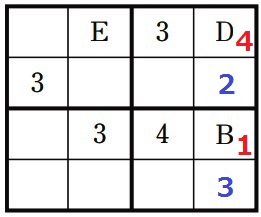
Ｂ＝１が確定。次にＤ＝４確定。
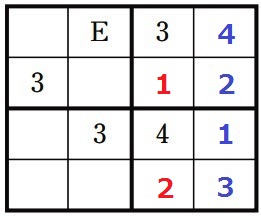
右半分が埋まる。
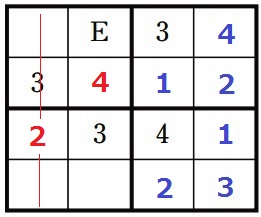
横の行を見てＥの下が４、その左下が２。
赤線のラインに２がこないので、左上の２×２マスからＥ＝２が確定。
Ｄ＝４、Ｅ＝２
（２）
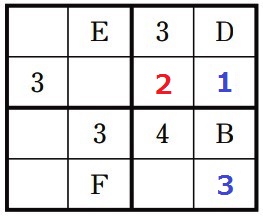
２が確定。
２の左が４、下が１。
縦と横からみてＦ＝２
（３）
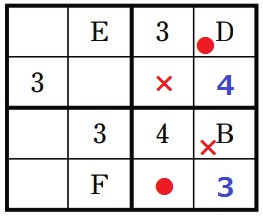
●と×が対応する。
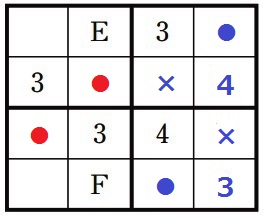
２つの●が確定。
残りの４マスは▲と■が対応する。
●と×に入る数は、１か２の２通り。
▲と■に入る数は、３か●でない数の２通り。
２×２＝４通り
（１）Ｃ＝２、（２）Ｃ＝１が各１通りずつだったので、
合計して６通り。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント