問題ＰＤＦ
（１）
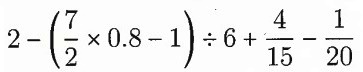を計算しなさい。
（２）
４％の食塩水110ｇに食塩を10ｇ加えてよくかき混ぜたあと、
できた食塩水を10ｇ捨てます。その後、水を何ｇか加えてよくかき混ぜたところ、
４％の食塩水ができました。このとき、水を何ｇ加えたか求めなさい。
（３）
１組から４組まである学校に通っているＡ、Ｂ、Ｃ、Ｄの４人が次のように話しています。
このとき、Ａの今年の組を答えなさい。ただし、昨年、今年ともにＡ、Ｂ、Ｃ、Ｄの４人のうち、
どの２人も同じ組にはいないものとします。
Ａ「４人中３人は昨年と今年で違う組になったね」
Ｂ「ぼくは昨年も今年も偶数組だった」
Ｃ「私は昨年も今年も同じ組だったわ」
Ｄ「私は昨年４組だった」
（４）
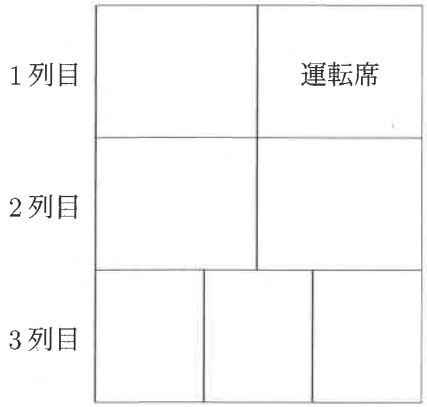
次の図のような、１列目と２列目は２人がけ、３列目は３人がけの７人乗りの車に、
大人３人、子ども４人が乗るときの座り方を考えます。
運転席には大人が座り、各列とも子どもが座る隣に最低１人の大人が座るとき、
座り方は何通りあるか答えなさい。
（５）
次の図は半径２ｃｍの円で、円周上の点は円周を12等分する点です。
１辺が１ｃｍの正方形をＡ、１辺が１ｃｍの正三角形をＢとするとき、
灰色部分の面積は、Ａが【あ】枚分の面積とＢが【い】枚分の面積の合計になります。
【あ】と【い】にあてはまる数をそれぞれ答えなさい。
＠解説＠
（１）
初手は0.8＝４/５に変換して分数計算。
以降は小数と分数を柔軟に切り替えながら処理すると、
２－３/10＋４/15－１/20
＝23/12
（２）
①４％食塩水110ｇの食塩…110×４％＝4.4ｇ
②食塩10ｇ追加→食塩水120ｇ、食塩14.4ｇ。濃度は14.4/120＝12/100＝12％
③食塩水10ｇ捨てる→食塩水110ｇ（濃度12％）
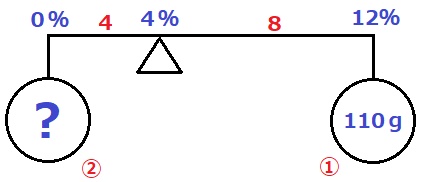
④水を混ぜる。水＝濃度０％として天秤を描く。
重さの比は支点からの距離の逆比→110×②＝220ｇ
（３）
推論は情報整理がカギ。
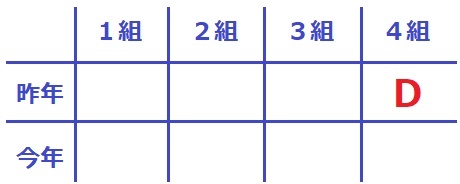
昨年４組がＤ。
４人中３人は違う組になり、Ｃは同じ組だった→Ａ・Ｂ・Ｄが違う組。
Ｂは昨年も今年も偶数組→昨年の偶数組は２組しかない→Ｂは昨年２組、今年４組が決まる。
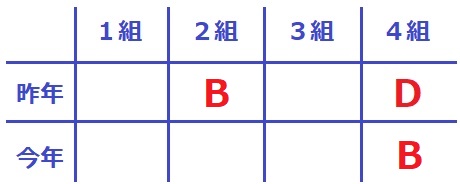
この先が１通りに決まらない。。
縦にＣＣと連続するので、場合分けして埋めてみると、
今年のＡは２組と確定できる。
（４）
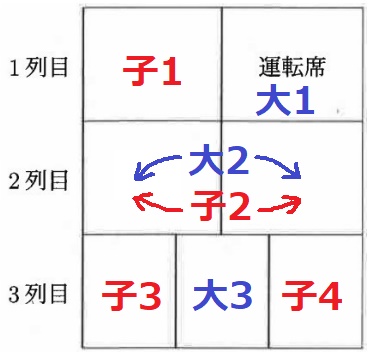
大人３人、子供４人。
子供の隣に必ず大人を配置するので、大人は各列に１人ずつ座らなければならない。
運転席は大人、２列目はいずれかが大人、３列目は子に挟まれて真ん中が大人。
大人１～３、子供１～４を順番に並べる（順列）。
さらに２列目で大人２と子供２の位置が２通りあるから、
３Ｐ３×４Ｐ４×２＝（３×２×１）×（４×３×２×１）×２＝288通り
（５）
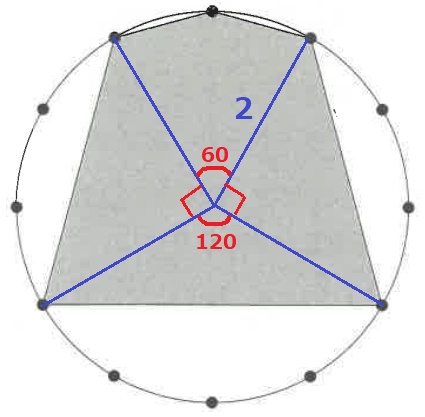
円の問題は中心から円周上の点に向けて半径を結ぶ。
円周の12等分から中心角がわかる。（円周１つ分＝360÷12＝30°）
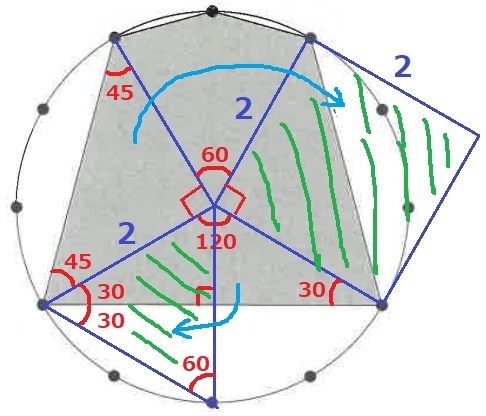
２つの直角二等辺三角形を合わせると、１辺２ｃｍの正方形になる。
→１辺１ｃｍの正方形（Ａ）４枚分。
下の三角形は内角が30°―30°―120°の二等辺三角形。
縦に割ってくっつけると１辺２ｃｍの正三角形になる。
→１辺１ｃｍの正三角形（Ｂ）４枚分。
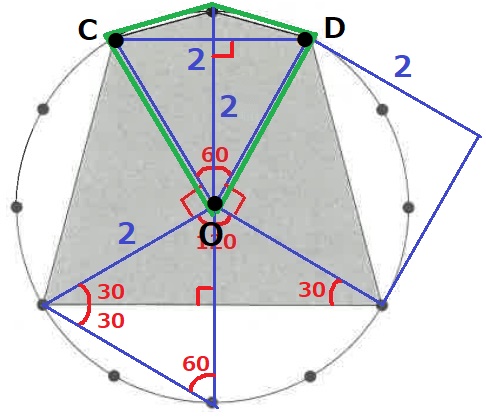
残りは直接、面積を求めにいく。
△ＯＣＤは正三角形→ＣＤ＝２ｃｍ
緑の四角形は２ｃｍの対角線が直交するので、２×２÷２＝２ｃｍ2→Ａ２枚分
合わせると、A６枚分とB４枚分。
あ…６、い…４
難関中（算数科）解説ページに戻る
コメント