問題ＰＤＦ
点Ａから出た光が正六角形ＡＢＣＤＥＦの辺に当たるたびに反射して、
どこかの頂点に到達するまで進みます。
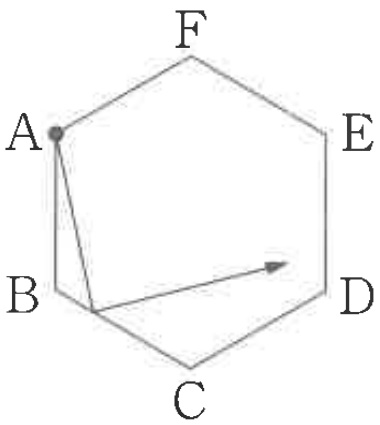
たとえば、点Ａから辺ＢＣの真ん中の点に光を向けると、１回反射して点Ｄまで進みます。
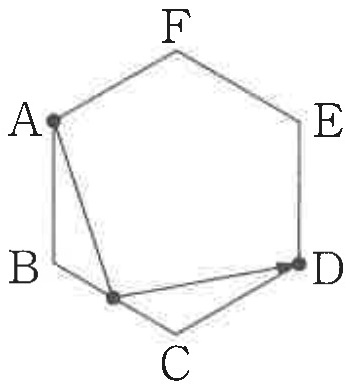
栄くん「ねえ、東さん。３回反射して点Ｂまで進む光を出すには辺ＢＣのどこに向ければいいかな？」
東さん「正六角形をつけたせばわかるんじゃないかな」
栄くん「１回反射して点Ｄまで進む光の道すじを考えたければ、
こういう正六角形を並べた図に１本の直線をかけばいいってことか！」
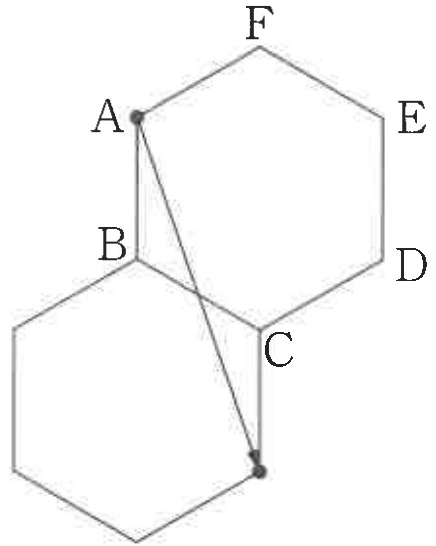
東さん「そう。これなら辺ＢＣの真ん中の点に向ければいいってわかる」
栄くん「じゃあ、図をかいて考えるね！ありがとう東さん！」
（１）
Ａから出て３回反射して点Ｂまで進む光の道すじを考えるときの１本の直線を図にかきなさい。
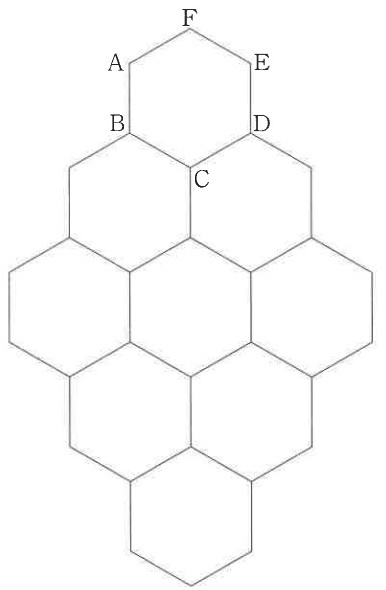
（２）
（１）のとき、光がはじめて辺ＢＣに当たる点をＧとします。
ＢＧ：ＧＣをもっとも簡単な整数の比で答えなさい。
＠解説＠
（１）
反射の問題は鏡の世界をつくる。
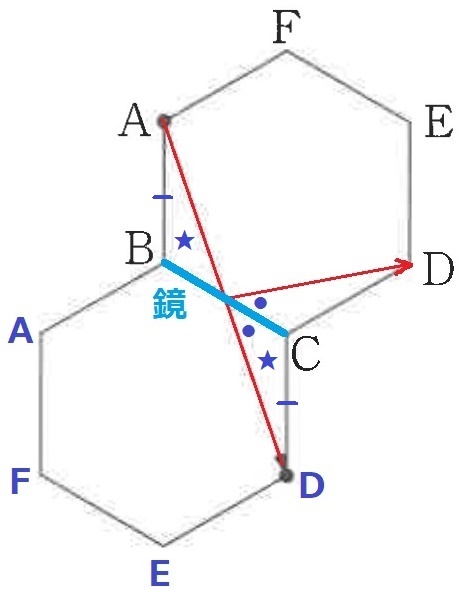
Ａから１回反射でＤに向かう。
光が反射するＢＣを鏡にして正六角形を対称移動させる。
鏡の世界のＤと直線で結ぶと、線対称により反射後の光を直進で表せる。
合同の三角形（★）から、光が反射する場所はＢＣの中点となる。
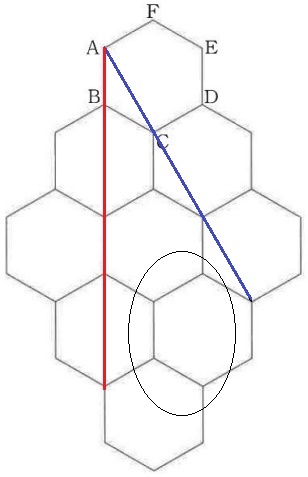
青線の右側は途中で２回しか交わらない＝２回しか反射しない。
赤線の左側は正六角形からはみ出してしまう。
２直線のあいだで３回交わりそうなこのあたりに見当をつける。
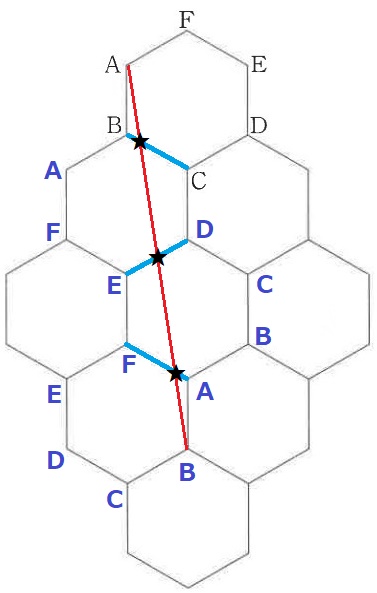
このように鏡を配置して正六角形を対称移動する。
途中の交点が３つであることを確認してＡとＢを結ぶ。
（２）
赤線の三角形が相似。
正六角形の１辺に着目して、ＢＧ：ＧＣ＝１：４
難関中（算数科）解説ページに戻る
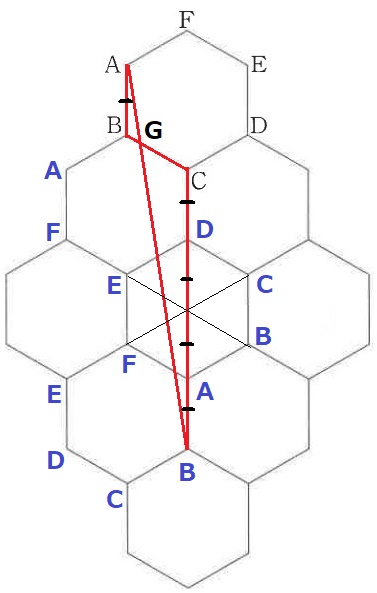
コメント