問題ＰＤＦ
下の図は、勝ち抜き戦で行われるあるサッカーの大会に、
11チームが参加した場合の組み合わせの例を表したものです。
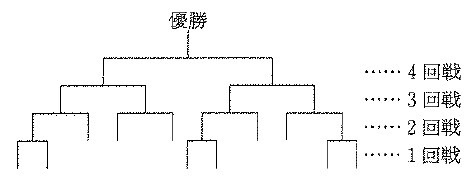
決勝戦は４回戦にあたり、６チームは１回戦から、残りの５チームは２回戦から参加します。
そのため、優勝するまでに、多いチームで４回、少ないチームで３回勝つ必要があります。
この大会の試合数について、決勝戦にあたる４回戦は１試合、３回戦は２試合、
２回戦は４試合、１回戦は３試合ありますから、全部で、
１＋２＋４＋３＝10（試合）
と求めることができます。また、勝ち抜き戦では１試合ごとに１チームずつ敗退し、
優勝するチームだけが最後まで敗退しませんから、
11－１＝10（試合）
と求めることもできます。
参加するチームの数が変わっても、優勝するまでに必要な勝ち数の差は１回以内にするものとして、
次の各問いに答えなさい。
（１）
この大会に25チームが参加する場合、１回戦から参加するチームの数は何チームですか。
（２）
決勝戦が６回戦にあたり、２回戦から参加するチームの数が９チームの場合、
参加するチームの数は全部で何チームですか。
＠解説＠
（１）
トーナメントにおける試合数はリード文にあるように【チーム数－１】
25チームであれば、25－１＝24試合
全体の試合数がわかったので、試合数に注目して考える。
決勝戦から試合数をさかのぼると、
決勝戦～２回戦までは１＋２＋４＋８＝15試合
１回戦の試合数は、24－15＝９試合
ということは、１回戦で試合をするチーム数は２×９＝18チーム
*７チームが２回戦から参戦することになる。
（２）
今度はチーム数で決勝戦からさかのぼる。
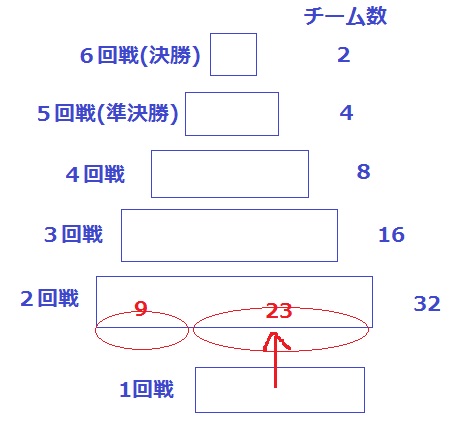
決勝戦に残るチームは２チーム。
そこから前へさかのぼると、２回戦に出場するチーム数は32チーム。
このうち、９チームが２回戦から参戦するので、
残りの32－９＝23チームが１回戦から勝ちあがってきたチーム。
１回戦で戦うチーム数は２×23＝46チームなので、
全体のチーム数は、46＋９＝55チーム
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント