問題PDF
太郎と次郎は黒い石と白い石をそれぞれ何個かずつ持っています。
2人の持っている石の合計数が等しいとき、次の問いに答えなさい。
(1)
太郎が持っている黒い石の半分を次郎にあげました。
その後、次郎が持っている黒い石の半分を太郎にあげました。
その結果、太郎の持っている黒い石は次郎の持っている黒い石より4個多くなりました。
太郎がはじめに持っていた黒い石は何個であったか答えなさい。
(2)
太郎が持っている白い石のうち5個を次郎にあげました。
その後、次郎が持っている白い石の4分の1を太郎にあげました。
その結果、太郎の持っている白い石ははじめより2個少なくなりました。
次郎がはじめに持っていた白い石は何個であったか答えなさい。
(3)
太郎がはじめに持っていた白い石と次郎がはじめに持っていた黒い石の和は27個でした。
太郎がはじめに持っていた白い石は何個であったか答えなさい。
@解説@
(1)
後ろから逆算して関係性を探る。
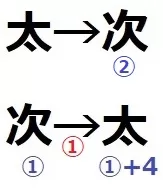
最終的に太郎は次郎より4個多くなった。
次郎を①個とすると、太郎は①+4個。
次郎は半分を太郎にあげたので、あげる前の次郎は②である。
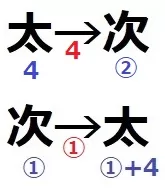
交換だから石の総和は変わらない。
太郎と次郎の和は、①+(①+4)=②+4
次郎にあげた後の太郎は、(②+4)-②=4個
太郎は半分の4個をあげたから、最初の太郎は8個。
(2)
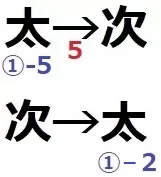
はじめの太郎を①とすると、最後の太郎は①-2個。
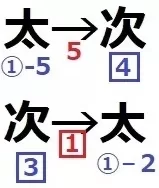
次郎は太郎に1/4をあげたから、太郎にもらった後の次郎を□4とすると、
□1を太郎にあげる。
太郎の個数の変化をみると、①-5+□1=①-2
□1=3
太郎からもらった後の次郎は、3×□4=12個
次郎が初めに持っていた数は、12-5=7個
(3)
前問の正解が条件。
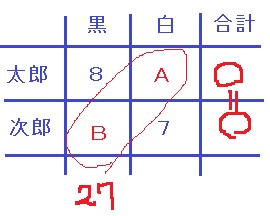
(1)より太郎の黒は8個、(2)より次郎の白は7個。
合計が一緒で8と7の差は1だから、AとBの差も1でA<B。
つまり、B-A=1
はじめに太郎が持っていた白い石(A)は、
(27-1)÷2=13個



コメント