問題PDF
下の図のように、点Oを中心とする1周720cmの円があります。
2点A、Bは円周上の点Pを同時に出発し、この円周上を、
点Aは時計回りに秒速40cm、点Bは反時計回りに秒速30cmで進みます。

(1)
出発後、A、O、Bが初めて一直線上に並ぶのは〔 〕秒後です。
(2)
出発後、A、Bが初めて点Pで出会うのは〔 〕秒後です。
(3)
3点P、A、Bを結んだ三角形が、出発後初めて二等辺三角形になるのは〔 〕秒後で、
2回目に二等辺三角形となるのは〔 〕秒後です。
@解説@
(1)
A・O・Bが一直線に並ぶ→AとBは正反対の位置にいる。
→AとBの移動距離の合計は半周360cm
AとBは1秒間に70cmずつ離れていくので、360÷70=36/7秒後
(2)
Aは、720÷40=18秒ごとにPに着く。
Bは、720÷30=24秒ごとにPに着く。
AとBが同時にPに着くのは、18と24の最小公倍数である72秒後。
(3)
手がかりは円周の長さとAとBの速さしかわかっていないので、
円周上でAとBが移動した距離から時間を計算する。
ポイントは、二等辺三角形ABPのどの2辺が等しくなるか。
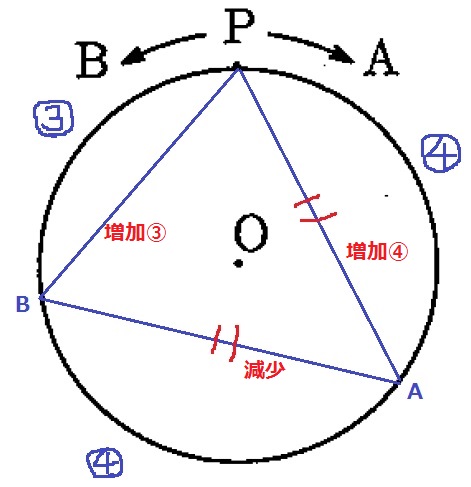
Pから同時に出発、Aの方が速い。
弧PBは③、弧PAは④の速さで長くなり、PA>PBの関係性が続く。
一方、Pを含まない弧ABは弧PA&PBより長かったが、
AとBが進むにつれて短くなっていく。
ということは、弧PAと、Pを含まない弧ABの長さが等しくなり、
AP=ABの二等辺がはじめにできる。
円周⑪=720cmになるので、Bが進んだ距離③=720×3/11=2160/11cm
Bは毎秒30cm動くので、2160/11÷30=72/11秒後
@@@
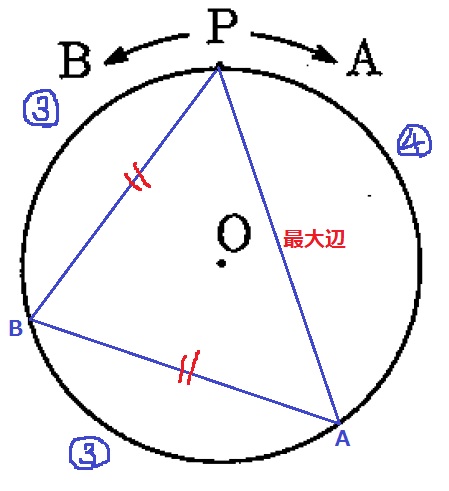
先ほどの状態から、引き続き3辺の長さがどう変化するかを見極める。
弧APと弧BPは長くなり、Pを含まない弧ABはさらに短くなっていく。
→2回目はBA=BPが等辺、APを最大辺とする二等辺。
円周⑩=720cm、③=720×3/10=216cm
216÷30=7.2秒後



コメント