問題ＰＤＦ
（１）
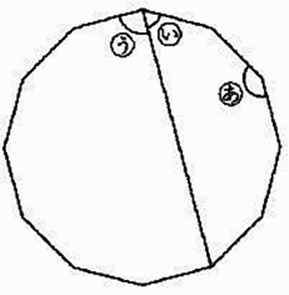
下は正十二角形に対角線を引いてつくった図形です。
（あ）、（い）、（う）の角の大きさをそれぞれ求めなさい。
（２）
部活動を終えた東さんが教室に入ったとき、
自分の机の上に次のような手紙が置いてあることに気づきました。
残念ながら、東さんは明日の朝から部活動の試合に出場するので栄くんに会って教えることができませんでした。そこで、解説の手紙を書いて栄くんの机の上に置くことにしました。その手紙が完成するように、解答用紙の空欄にあてはまる数や言葉を書き込みなさい。また、《説明を記す欄》には、前後の文章とつながるように説明を書きなさい。
＠解説＠
（１）
（あ）は正十二角形の内角の１つ。
ｎ角形の内角の和→180×（ｎ－2）
180×（12－２）÷12＝150 …（あ）
＠別解＠
多角形の外角の和は360°
正多角形の外角はそれぞれ等しい。
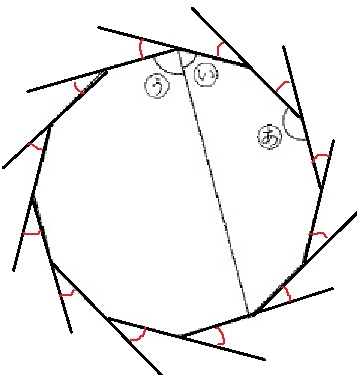
赤い印は同じ角度だから、360÷12＝30°
180－30＝150°
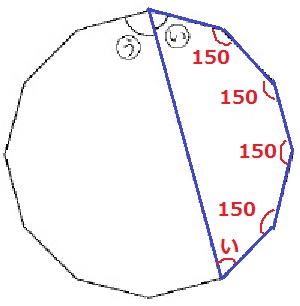
右側の六角形で考える。
六角形の和→180×（６－２）＝720°
（720－150×４）÷２＝60° …（い）
正十二多角形の内角の１である（あ）から（い）を引けば（う）。
150－60＝90° …（う）
（２）
解答用紙の誘導に従う。
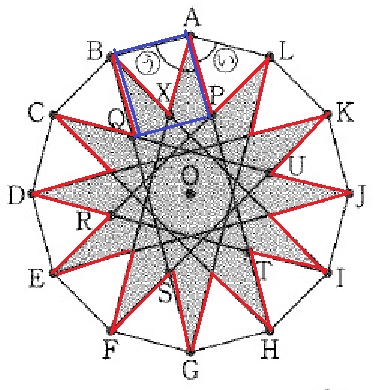
△ＡＢＸにおいて、（い）＝60°だから、
∠ＸＡＢ＝∠ＸＢＡ＝60°
残りの角度の∠ＡＸＢ＝60°となり、△ＡＢＸは正三角形となる。
色のついた部分の周囲（赤線の合計）が72ｃｍ。
外側の三角形はすべて合同な正三角形なので、１辺の長さがそれぞれ等しい。
ＡＢ＝72÷24＝３ｃｍ
四角形ＡＢＱＰにおいて、（う）＝90°だから、
∠ＰＡＢ＝∠ＱＢＡ＝90°
残りの角度も対称性から∠ＢＱＰ＝∠ＡＰＱ=90°
さらに、合同な正三角形の１辺より、ＡＢ＝ＡＰ＝ＢＱ
ここから、四角形ＡＢＱＰは正方形となる。
正方形ＡＢＱＰの１辺ＡＢが３ｃｍなので、
３×３＝９ｃｍ2
六角形ＰＱＲＳＴＵを作図。
これを６つに分割する。
ＡＢ＝ＰＱから１つの正三角形は外側の正三角形（△ＡＢＸ）と合同になる。
よって、六角形ＰＱＲＳＴＵの面積は三角形ＡＢＸの面積の６倍。
中の正三角形をすべて外側に移動させると、斜線部分の面積は赤い正方形６つの面積の和となる。
正方形の１つは９ｃｍ2なので、９×６＝54ｃｍ2
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント