PDF問題
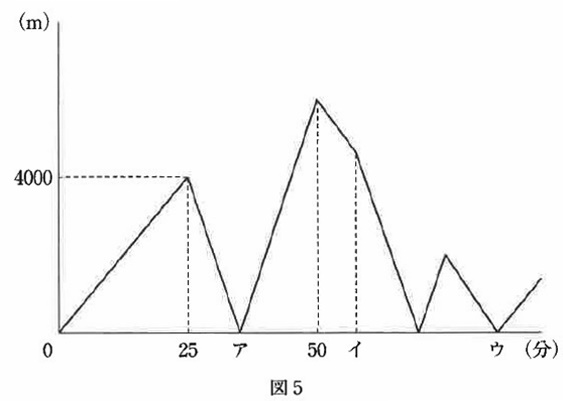
太郎君と花子さんは同時にP地点を出発し、P地点とQ地点の間のまっすぐな道を何度も往復しました。2人が出発してから初めて出会ったのは太郎君がQ地点を折り返してきて、P地点から測ってQ地点までの距離の3/5のところでした。図5は、2人が出発してからの時間(分)と2人の間の距離(m)の関係を表したものです。
(1)
太郎君と花子さんの速さの比を最も簡単な整数の比で表しなさい。
(2)
太郎君の速さは毎分何mですか。
(3)
P地点からQ地点までの距離は何mですか。
(4)
グラフのア、イ、ウにあてはまる数をそれぞれ求めなさい。
@解説@
(1)
初めて出会った場所に注目する。
速さの比=進んだ距離の比
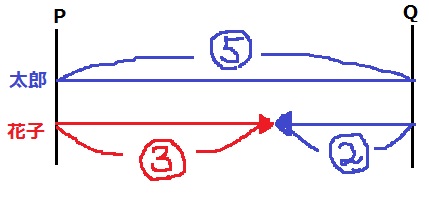
太郎:花子=7:3
(2)(3)
グラフ上の〔25分4000m〕は、太郎がQに着いて折り返したとき。
今度は太郎が進んだP-Q間を⑦とおく。花子の進む距離は③。
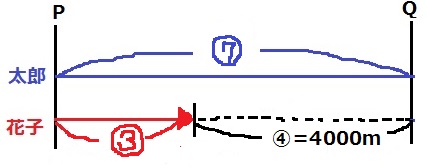
④=4000m
P-Q間の距離は、4000×⑦/④=7000m…(3)の答え
太郎の速さは、7000m÷25分=分速280m…(2)の答え
(4)
花子の速さは、280×3/7=分速120m

アは、太郎と花子が初めて出会ったとき。
2人の進む距離の合計は、P-Q間の距離の2倍(往復)
7000×2÷(280+120)=35分
25の倍数で太郎はPとQ地点に着く。
50分後に太郎はPに戻ってくる。
イは花子がQ地点に着いたとき。
以降、太郎と花子は出会いに行くので、2人の間の距離は急速に縮まる。
7000m÷分速120m=175/3分…イ
ウは、太郎と花子が3回目に会うとき。
出会う形であれば、2人の進む距離の合計はP-Q間の往復距離の倍数になるが、
3回目は太郎が花子を追い越す形になるので、地道に計算するしかない。
隔たりグラフをダイヤグラムに直してみよう。

太郎が青、25の倍数で行ったり来たり。
花子が赤。175/3の倍数で行ったり来たり。
赤と青が交差する地点で2人の距離が0mとなる。

△ABCと△EDCに注目。
AB=75-175/3=50/3
ED=175/3×2-100=50/3
AB=EDで、AB//DEから錯角が等しく、一辺両端角で合同。
CはBDの中点となる。
75+(100-75)÷2=175/2分…ウ



コメント