2018年度　栄光学園中学過去問【算数】大問４解説

問題ＰＤＦ
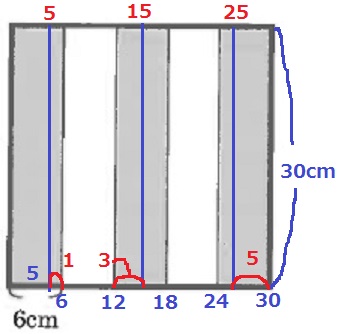
１辺の長さが30ｃｍの正方形の透明な３枚のガラス板Ａ、Ｂ、Ｃがあります。図１のように、ガラス板はそれぞれ等分され、色のついている部分と色のついていない部分が交互になっています。

２枚のガラス板を重ねたとき、色のついている部分が重なっていると色は濃く見えます。例えば、ガラス板Ｂとガラス板Ｃを図１と同じ向きでぴったりと重ねると、図２のように色の濃く見える部分が４ヶ所あります。
 
（１）
固定したガラス板Ａの上にガラス板Ｂを図１と同じ向きでぴったりと重ね、
ガラス板Ｂを右に秒速１ｃｍで30秒間動かしていきます。

①
５秒後に色の濃く見える部分の面積の和を答えなさい。

②
ガラス板Ｂを動かしても、色の濃く見える部分の面積の和が変化しないときがあります。それは動かし始めてから何秒後から何秒後の間ですか。考えられるものをすべて求め、下の例にならって答えなさい。
（答え方の例）
３秒後から５秒後の間と、10秒後から13秒後の間の場合：（３～５）（10～13）

（２）
固定したガラス板Ａの上にガラス板Ｃを図１と同じ向きでぴったり重ね、ガラス板Ｃを右に秒速１ｃｍで30秒間動かしていくとき、ガラス板Ｃを動かしても色の濃く見える部分の面積の和が変化しないときがあります。それは動かし始めてから何秒後から何秒後の間ですか。考えられるものをすべて求め、（１）②と同じように答えなさい。

＠解説＠
麻布で類題が出題された調べ上げ問題。
（１）①

ここは確実に取りたい。
先に６の倍数ごとに目盛りをうち、左５ｃｍから15ｃｍ、25ｃｍに線をひく。
重なっているところの底辺の合計は９ｃｍ。
９×30＝270ｃｍ²

②
しんどい(´Д｀)
捨て問の登場が早すぎる。

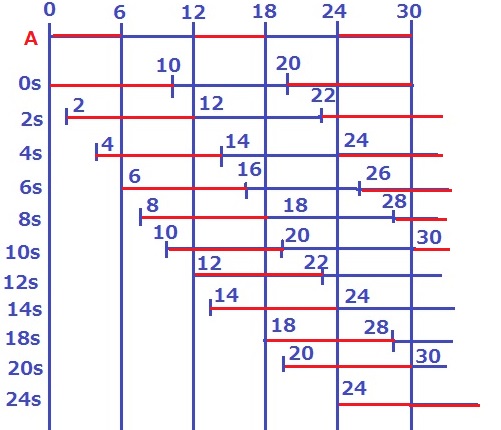
がんばりました(;´Д｀)
だいたい２秒ごとに状況が変わる。
24秒後～30秒後は重なるところの面積が減っていくので除外。

ガラス板Ａの色が付いている部分を左から①・②・③として、
重なっているところの面積の変化をみていく。
減少と増加が１つずつのところは変化がない。
よって、（２～４）（６～８）（10～12）（14～18）（20～24）

（２）
前問の図を描けていることが、正解への前提条件。
ガラスＣは、ガラスＢでは空白であった真ん中に10ｃｍ分が追加される。
両サイドは30ｃｍから20ｃｍに短くなるが、
本問は面積の変化が問われており、両サイドの変化は前問と同じだから考えない。
→答えの候補は先ほどの解答に絞られる。
そのなかから、真ん中の10ｃｍ部分の変化に神経をとがらせる。

↑10ｃｍ部分に丸をつけてみた。
（２～４）では、②で減少する。
（６～８）では、②が減少して③が増加→変わらない。
（10～12）では、③の部分とフル被りで変わらない。
（14～18）では、③が減少する。
（20～24）では、右にフェードアウト済みなので変わらない。
よって、（６～８）（10～12）（20～24）
難関中（算数科）解説ページに戻る