問題PDF
ある高層ビルの屋上には、図のような直径7mの円周の半分と、長さ22mの直線を組み合わせた形の展望コースがあり、C地点はB地点の真東の方向にあります。身長180cmの父と身長120cmの子どもがこのコース上をA地点からC地点まで、それぞれ一定の速さで歩きます。ただし、A地点とB地点を結ぶ、図の点線は半円の直径です。円周率を22/7として、次の問いに答えなさい。

(1)
ある日、子どもがA地点を出発し、父がそのS秒後にA地点を出発しました。父はB地点で子どもを追いこし、さらにT秒後にC地点に到着しました。このときS:T=11:76でした。
(ⅰ)父と子どもが歩く速さの比を、最も簡単な整数の比で答えなさい。
(ⅱ)父が子どもを追いこしてから7秒後に、太陽は真東の方角に出ており、太陽による二人の影の先端がB地点から3.2m真東の地点で重なりました。父の歩く速さは毎秒何mですか。
(2)
別のある日、子どもがA地点を出発し、その後、父がA地点を出発しました。前を行く子どもがB地点を通過するまでに太陽による二人の影の先端が重なり、そのとき、子どもの影の長さは7mでした。影の先端が重なってから何秒後に父が子どもを追いこしますか。ただし、二人が歩く速さは(1)(ⅱ)の速さと等しいものとします。
@解説@
(1)(ⅰ)

先に距離を求めておく。
AB間は、7×22/7÷2=11m
S:Tの時間の比を【 】で示すと、子が先に【11】の時間を歩き、
父が子を追い越したB地点からC地点に着く赤い矢印の時間が【76】となる。

ABとBCの距離の比は、11:22=1:2
距離の比と時間の比は比例。
父はAB間を【76】÷2=【38】の時間で歩いた。
言い換えれば、青い矢印が【38】となる。
AB間を父は【38】、子は【49】の時間で歩いたので、
速さは時間の比の逆比だから、父:子=49:38
(ⅱ)
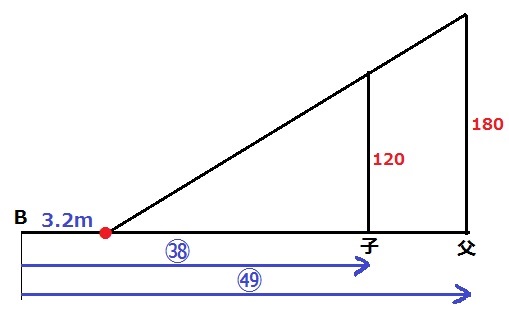
位置関係を正確に図示する。
B地点のあと、両者は東を歩く。
太陽は真東にあるから、影は西側へ伸びる。
前問より、速さの比がわかっているので、
B地点からの距離の比は、父:子=㊾:㊳
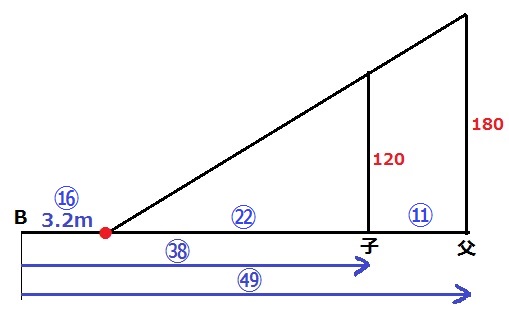
子と父のあいだの距離は、㊾-㊳=⑪
三角形の相似で120:180=2:3から、
影の先端●と子の距離は、⑪×2=㉒
B地点から●の距離は、㊳-㉒=⑯
父は㊾を7秒で進むから、父の速さは、3.2×㊾/⑯÷7=毎秒1.4m
(2)
発想力が問われる。
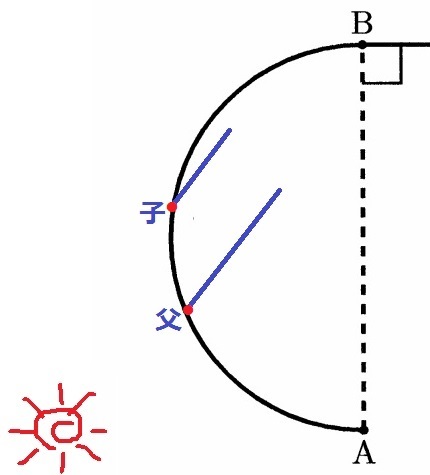
影は太陽の反対側にできる。
父と子の影は平行線となるが、半円上のコースで重なるのはどういう場合だろう?

父の影の延長線上に子がいればいい。
しかし、父と子のあいだの距離は弧である。
はたして、扇形の中心角を算数の範囲で求められるのか。。
新たに与えられた情報は、『子の影の長さは7m』
ということは、前問の相似比から父と子の直線距離は7/2m…
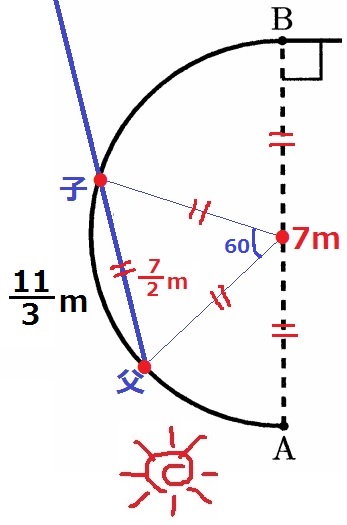
円の直径ABが7mであることを思い出す。
父と子の直線距離は円の半径に相当する。
半径7/2mを1辺とする正三角形を描くと中心角が60°だから、
父と子のコース上の距離は半円の3分の1にあたる11/3m。
父の速さは毎秒1.4m。
子の速さは、1.4×38/49=毎秒38/35m
1秒あたり、1.4-38/35=11/35m近づくので、
父が子を追い越すのは、11/3÷11/35=35/3秒後



コメント