問題ＰＤＦ
赤、青、黄、緑の４色を点灯することができるライトを４つ、左から一列に並べます。
この４つのライトは、スイッチを押すたびにある規則にしたがって色が切り替わります。
例えば、上の図のように
赤を青、青を青、黄を緑、緑を赤
に切り替わるような規則を定めると、スイッチを押すたびに、
この規則にしたがって色が変わっていきます。
はじめ、ライトは左から順に赤、青、黄、緑に点灯しています。
次の各問いに答えなさい。
（１）
はじめの状態からスイッチを１回押したとき、
異なる４色のライトが点灯するような規則は何通り作れますか。
（２）
はじめの状態からスイッチを２回続けて押したとき、
ライトが左から順に赤、青、黄、緑に点灯するような規則は何通り作れますか。
（３）
はじめの状態からスイッチを３回続けて押したとき、
４つのライトは初めて赤一色になりました。このような規則は何通り作れますか。
＠解説＠
（１）
点灯の規則を答えるが、初期状態が異なる４色であり、
スイッチを１回押したあとの結果も異なる４色ということは、
とどのつまり、４色の配置換えである。
順列の考えで、4Ｐ4＝24通り
（２）
２回押して元に戻る。
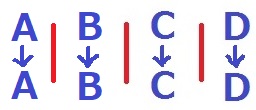
同色を維持。１通り
２色を交換して元に戻る。
Ａを赤とすると、赤とペアになるＢが決まれば全て決まる。
Ｂは赤以外の３通り。
（*４人を２チームに分ける考え方で、4Ｃ2÷２＝３でもＯＫ）
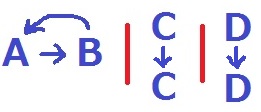
１ペアを交換にして、残りの２色を同色維持にする。
交換する２色を選ぶ。4Ｃ2＝６通り
計10通り。
（３）
３回押したら初めてすべて赤になった。
奇数回なので、先ほどのように２色の交換では戻れない。
先に赤から始まり赤で終わるパターンを考える。
わかりやすいのは、赤→赤の規則で同色を維持する【赤→赤→赤→赤】
異色を経由するのはどうか？
２色の交換は無理なので、赤→青→黄…の３色で試すと、
青と黄は１周して元の色に戻るので、赤にすることができない！
ということは、赤→赤が確定。
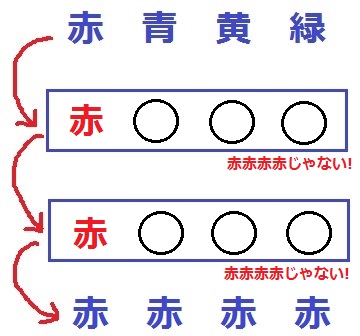
もう１つ配慮すべきは、３回押したあとに初めて赤一色になった点。
途中で赤赤赤赤にはならない。
一度、赤にすれば赤が継続する。
３色を３手目で全て赤にするには、１個ずつ順番に赤に変えていく他ない。
青黄緑のうち、１手目で赤にする色、２手目で赤にする色、３手目で赤にする色を選ぶ。
順列の考えで、3Ｐ3＝３×２×１＝６通り
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント