2020年度　渋谷教育学園幕張中学過去問【算数】大問５解説

問題ＰＤＦ
図のように底面が正方形の角すいＰ－ＡＢＣＤがあります。
三角形ＡＰＢと三角形ＡＰＤはどちらも角Ａが直角の直角三角形です。
４つの辺ＡＢ、ＢＣ、ＣＤ、ＤＡ上にそれぞれ点Ｑ、Ｒ、Ｓ、Ｔをとります。
直線ＱＳと直線ＡＤ、直線ＴＲと直線ＡＢはそれぞれ平行で、ＢＲ：ＲＣ＝ＡＱ：ＱＢです。

このとき、次の各問いに答えなさい。
ただし、角すいの体積は（底面積）×（高さ）÷３で求められるものとします。
また、立体のすべての面の面積をたし合わせたものを表面積といいます。

（１）
辺ＡＰ、ＡＢ、ＰＢの長さがそれぞれ４ｃｍ、３ｃｍ、５ｃｍのとき、
角すいＰ－ＡＢＣＤの表面積は何ｃｍ²ですか。

（２）
この立体を点Ｑと点Ｓを通るように底面に垂直な平面で切り、
さらに点Ｔと点Ｒを通るように底面に垂直な平面で切り、切り取ってできた面にだけ色をぬります。
点Ａ、Ｂ、Ｃを含む立体をそれぞれ立体Ｘ、Ｙ、Ｚとし、
立体Ｙと立体Ｚの体積の比を４：１とするとき、次の各問いに答えなさい。
①
立体Ｘと立体Ｚの体積の比をもっともかんたんな整数の比で表しなさい。

②
立体Ｚにおいて、色をぬった部分の面積と、色をぬっていない部分の面積の比が１：４のとき、
立体Ｘと立体Ｚの表面積の比をもっともかんたんな整数の比で表しなさい。

＠解説＠
（１）

∠ＡＢＣ＝∠ＰＡＢ＝90°→面ＰＡＢとＢＣは垂直→∠ＰＢＣ＝90°
３×４÷２×２＋３×５÷２×２＋３×３＝36ｃｍ²

（２）①
Ｙ：Ｚの体積比しかわかっていないという…。
おまけにＹの三角柱は横を向いており、側面の三角形の面積がわからず、
ＢＲ：ＲＣ＝ＡＱ：ＱＢの値も不明でもどかしさに駆られる(´･_･`)

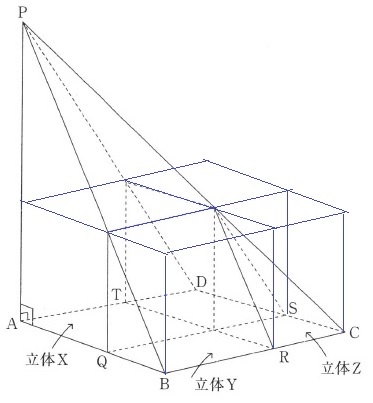
上図のような補助線をひく。
ポイントは、すべてを直方体に変えてしまうこと！
同じ図形に統一すれば、辺の比が出しやすくなる。

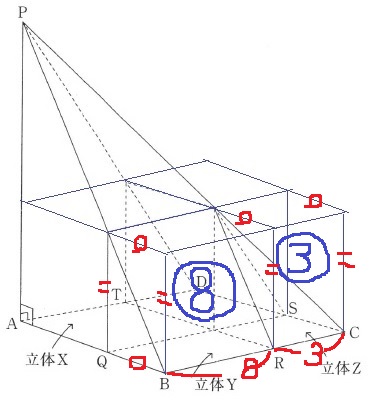
体積比は、Ｚ：Ｙ＝①：④
奥の直方体は四角錘Ｚの３倍なので、①×３＝③
手前の直方体は、三角柱Ｙを２倍したもので、④×２＝⑧
２つの直方体は高さと奥行きの長さが共通しており、
横の辺であるＢＲ：ＲＣの比が体積比８：３と符合する。

△ＰＡＢ∽△ＵＱＢより、ＵＱ＝□３とすると、ＰＡ＝□11
立体Ｚの体積…③×③×□３＝【27】
全体の体積（四角錘Ｐ－ＡＢＣＤ）…⑪×⑪×□11＝【1331】

立体Ｘは、全体から立体Ｙ２つと立体Ｚをひく。
立体Ｙ：立体Ｚ＝４：１より、立体Ｙの２つ分の体積…【27】×４×２＝【216】
立体Ｘの体積…【1331】－【216】－【27】＝【1088】
したがって、立体Ｘ：立体Ｚ＝1088：27

②
今度は表面積を求める。与えられた情報は、
『立体Ｚにおいて、色が塗られた２面と塗られていない３面の表面積の比が１：４』
立体Ｚの底面積は１辺③の正方形。
前問の体積では高さの比を□としたが、これを○で統一して計算したい。

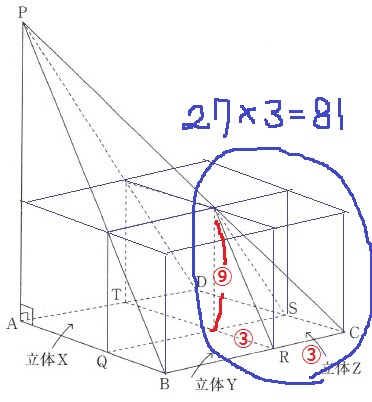
立体Ｚの体積は【27】で、底面積と高さを同じにする直方体の体積は【81】
この高さは、【81】÷（③×③）＝⑨

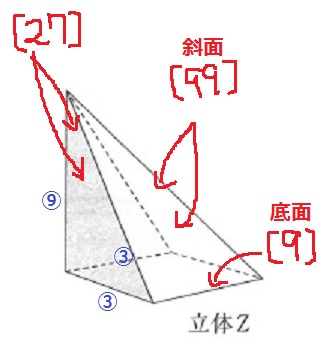
つづいて、立体Ｚを検証。
立体Ｚで色が塗られている部分の表面積は、③×⑨÷２×２＝〔27〕
立体Ｚの表面積は問題文の１：４より〔27〕×５＝〔135〕
（*部位に分けると上のようになるが、まとめて処理できるので出さなくても可）

立体Ｚと、〇で囲った上部の四角錘が相似。
辺の比が③：⑧なので、面積比はその２乗になる。
〔135〕×（⑧×⑧）/（③×③）＝〔960〕
これは、上の４つの面と、底面の★を合わせた表面積の和。
下の直方体の側面（●４つ）は、⑧×⑨×４＝〔288〕
立体Ｘの表面積は、〔960〕＋〔288〕＝〔1248〕
よって、立体Ｘ：立体Ｚ＝1248：135＝416：45

これを試験時間内に終わらせるのはシビア(;^ω^)
難関中（算数科）解説ページに戻る