問題PDF
立体のいくつかの辺を切って開いたときの展開図について考えます。
例えば、図1の立方体において、太線で示した7つの辺を切って開くと、図2のような展開図になります。
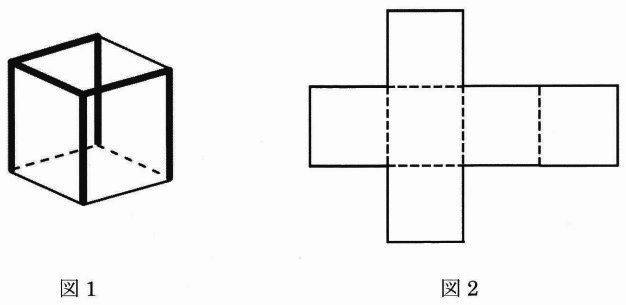
(1)
図3は正三角形4面で囲まれた立体です。
いくつかの辺を切って開いて図4のような展開図を作るためには、どの辺を切ればよいですか。
解答欄の図に太線で示しなさい。

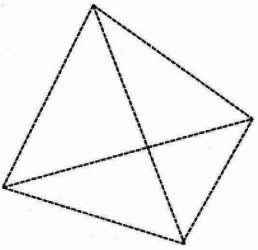
(2)
図5の立方体において、太線で示した辺を切って開くと、
どのような展開図になりますか。その展開図をかきなさい。


(3)
立体の辺を切って展開図を作るとき、切った辺の本数とその長さの合計を考えます。
例えば、(2)の立方体の1辺の長さを10cmとした場合、切った辺の本数は7本、長さの合計は70cmです。
図6のような角柱のいくつかの辺を切って展開図を作ります。
角柱の底面は1辺の長さが10cmの正五角形で、高さは15cmです。
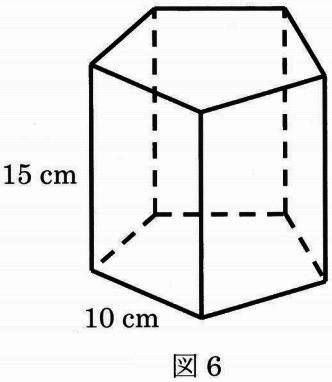
①
切った辺の長さの合計が最大になるときの、切った辺の本数とその長さの合計を答えなさい。
②
切った辺の長さの合計が最小になるときの、切った本数とその長さの合計を答えなさい。
(4)
図7は正五角形12面で囲まれた立体です。
何本の辺を切れば展開図を作ることができますか。
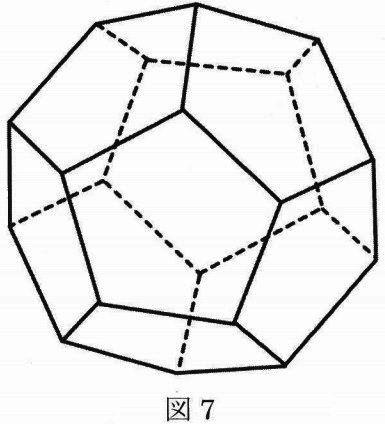
@解説@
(1)
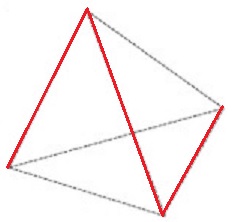
*これ以外にもあります。

4つの三角形が一直線に並ぶように三角錐を切る。
展開図の周りが6辺だから、6÷2=3辺分切る。
端っこの2つの三角形は2辺、なかの2つは1辺が切られる。
切られない3つの辺に注目するのもいい。
(2)


回転や反転させた展開図でもOK。
手前の面から出発するとやりやすいかな?
完成した展開図がきちんと立方体になるか確かめよう。
(3)①
15cmを優先してカット。
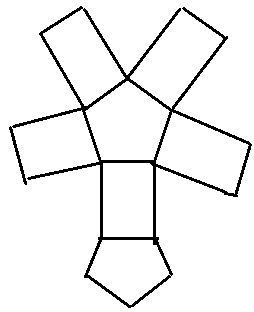
↑こんなイメージ。
切った辺の本数…9本
長さの合計…15×5+10×4=115cm
②
今度は10cmを優先してカット。

切った辺の本数…9本
長さの合計…10×8+15=95cm
(4)
正十二面体の展開図を作るために、何本の辺を切るべきか。
今までの設問が誘導になっている。
(1)正四面体
面…4個 頂点…4個 辺…6本 切った本数…3本
(2)正六面体(立方体)
面…6個 頂点…8個 辺…12本 切った本数…7本
(3)正五角柱
面…7個 頂点…10個 辺…15本 切った本数…9本
(4)正十二面体
面…12個
辺…正五角形が12個で隣同士で辺を共有するから、
5×12÷2=30本
頂点…【面の数+頂点の数-辺の数=2】(オイラーの多面体定理)
12+□-30=2 □=20個
規則がないか調べてみると、
【(頂点の数+辺の本数-面の数)÷2=切った本数】という規則にありつける。
よって、(20+30-12)÷2=19本
@別解@
もっと簡単な方法がある。


展開図をよく見ると、正三角錐は面4つで切らない辺が3つ。
正六面体は面6つで切らない辺が5つ。
植木算のあいだの数のように考えると、面がつながる場所=切らない辺の数=〔面の数-1〕
正十二面体で切らない辺の数は12-1=11本
よって、切るべき辺の数は、30-11=19本
@よくみたら・・@
【切るべき辺の数=頂点-1】
20-1=19本
先ほどのオイラーの多面体定理を使います。
【面の数+頂点の数-辺の数=2】
*辺の数=切る辺の数+切らない辺の数
*切らない辺の数=面の数-1
面+頂点-(切る辺+切らない辺)=2
面+頂点-(切る辺+面-1)=2
面+頂点-切る辺-面+1=2
頂点-1=切る辺



コメント