2023年度　聖光学院中学過去問【算数】大問２解説

問題ＰＤＦ
下の図のような、ＡＢ＝ＡＣ＝10ｃｍ、ＢＣ＝12ｃｍの二等辺三角形ＡＢＣがあります。
はじめに点Ｐは点Ｂの位置に、点Ｑと点Ｒは点Ｃの位置にあり、３点Ｐ、Ｑ、Ｒは同時に移動を開始し、点Ｐと点Ｑは点Ａへ向かって辺上を毎秒１ｃｍの速さで、点Ｒは点Ｂへ向かって辺上を毎秒〔　ア　〕ｃｍの速さで移動します。直線ＱＲは常に辺ＡＢに平行であるとき、次の問いに答えなさい。

（１）
〔　ア　〕にあてはまる数を答えなさい。

（２）
三角形ＡＰＱと三角形ＱＲＣの面積について、面積の大きいほうが小さいほうの25倍になるのは、
３点Ｐ、Ｑ、Ｒが移動を開始してから〔　イ　〕秒後です。
〔　イ　〕にあてはまる数として考えられるものをすべて答えなさい。

（３）
３点Ｐ、Ｑ、Ｒが移動を開始してから５秒後の３点の位置をそれぞれＰ₅、Ｑ₅、Ｒ₅とし、
８秒後の３点の位置をそれぞれＰ₈、Ｑ₈、Ｒ₈とします。
直線Ｐ₅Ｑ₅とＰ₈Ｒ₈の交点をＸ、直線Ｐ₅Ｒ₅のとＰ₈Ｒ₈の交点をＹ、直線Ｐ₅Ｒ₅とＱ₈Ｒ₈の交点をＺとします。
このとき、直線ＡＲ₅の長さは８ｃｍとなります。

①三角形Ｐ₅ＸＹの面積は何ｃｍ²ですか。
②直線ＹＺの長さは何ｃｍですか。

＠解説＠
（１）

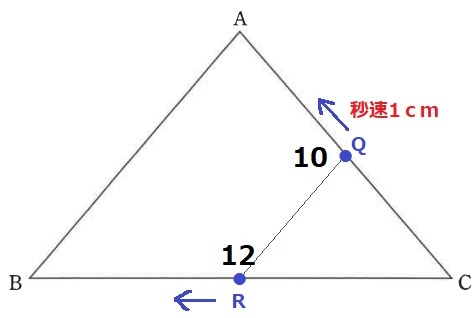
ＱＲは常にＡＢと平行である。
Ｑの速さは毎秒１ｃｍだから、10秒後にＡに着く。
同時にＲはＢに着く。Ｒの速さは、12ｃｍ÷10秒＝秒速1.2ｃｍ

（２）

ＡＰとＱＲは平行。
また、ＰとＱは対称的な動きをするのでＰＱとＢＣ（ＲＣ）も平行。
→△ＡＰＱと△ＱＲＣは２角が等しく相似。
【面積比１：25→相似比１：５】
△ＱＲＣが小さい場合、ＡＱ：ＱＣ＝⑤：①
ＱＣ＝10×①/⑥＝５/３ｃｍ→５/３秒後

もう１つは△ＡＰＱが小さい場合。
ＱＣ＝10×⑤/⑥＝25/３ｃｍ→25/３秒後
５/３秒後と25/３秒後

（３）①
ここから差がつく。

問題文に従って、Ｘ・Ｙ・Ｚを記入する。（間違えないように！）
△Ｐ₅ＸＹを求めたい。
ＸとＹに関する比が欲しい…。

（ＢはＰ₀、Ｒ₁₀にあたる）
Ｐ₈Ｐ₅：Ｐ₅Ｂ＝３：５
△Ｐ₈Ｐ₅Ｘと△Ｐ₈ＢＲ₈は相似で、Ｐ₅Ｘ＝③とするとＢＲ₈＝⑧
ＢＲ₈：Ｒ₈Ｒ₅＝２：３だから、Ｒ₈Ｒ₅＝⑧×３/２＝⑫
△Ｐ₅ＹＸと△Ｒ₅ＹＲ₈の相似から、Ｐ₅Ｙ：ＹＲ₅＝①：④

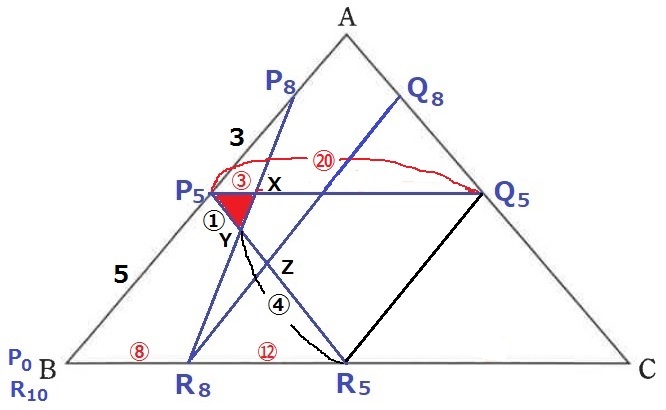
Ｑ₅Ｒ₅に補助線。
四角形Ｐ₅ＢＲ₅Ｑ₅に着目すると、２組の対辺が平行な平行四辺形。
Ｐ₅Ｑ₅＝ＢＲ₅＝⑳

5がつく点はそれぞれの△ＡＢＣの辺の中点で、
△Ｐ₅Ｒ₅Ｑ₅の面積は△ＡＢＣの４分の１にあたる。
方針；【△ＡＢＣ⇒△Ｐ₅Ｒ₅Ｑ₅⇒△Ｐ₅ＸＹ】
△ＡＢＣの底辺はＢＣ＝12ｃｍ、高さはＡＲ₅＝８ｃｍだから、
12×８÷２÷４×③/⑳×①/⑤＝９/25ｃｍ²

②

ＹＺを１辺とする△ＹＲ₈Ｚと相似にあるのは△ＹＰ₈Ｐ₅。
対応する辺の長さを調べる。
Ｐ₈Ｐ₅＝３ｃｍ、Ｐ₅Ｂ＝５ｃｍ
△Ｐ₅ＢＲ₅と△ＺＲ₈Ｒ₅は相似→ＺＲ₈＝５×③/⑤＝３ｃｍ
△ＹＲ₈Ｚと△ＹＰ₈Ｐ₅の相似比はＺＲ₈：Ｐ₅Ｐ₈＝１：１
ＹはＰ₅Ｚの中点である。

四角形ＡＰ₅ＺＱ₈に着目する。
ＡＢとＱＲは常に平行だから、ＡＰ₅とＱ₈Ｚは平行。
Ｐ₅とＲ₅はそれぞれＡＢとＢＣの中点→Ｐ₅Ｒ₅とＡＣ（Ｐ₅ＺとＡＱ₈）も平行。
２組の対辺が平行だから平行四辺形。
Ｐ₅Ｚ＝ＡＱ₈＝２ｃｍ
ＹＺ＝２÷２＝１ｃｍ

＠別解＠
二等辺三角形Ｐ₅ＢＲ₅、ＺＲ₈Ｒ₅から、Ｐ₅Ｒ₅＝５ｃｍ、ＺＲ₅＝３ｃｍ
Ｐ₅Ｚ＝５－３＝２ｃｍでも出せました。
難関中（算数科）解説ページに戻る