問題PDF
図1のようなコースを作り、おもちゃの電車を走らせることにしました。電車は駅から出発し時計回りに走ります。また、駅に戻ってくると5秒間停車して再び出発します。
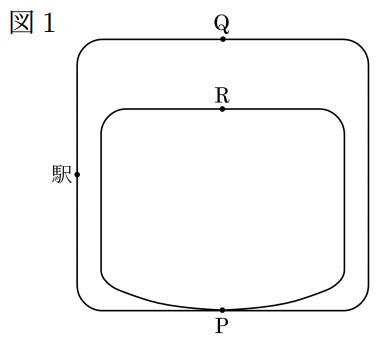
コースは外側の1周540cm、内側の1周400cmからなり、外側と内側のコースは地点Pのポイント1点でつながっており、ポイントが切り替わることで電車が異なるコースを走ることができます。図のように外側のコースには、地点Pからコースに沿って135cmの位置に駅が、地点Pからコースに沿って270cmの位置に地点Qがあり、内側のコースには、地点Pからコースに沿って200cmの位置に地点Rがあります。
電車Aと電車Bは外側のコースを走るときは秒速30cm、内側のコースを走るときは秒速20cmで進み、地点Pのポイントを通過した瞬間に速さが変わり、それぞれのコースを一定の速さで走るものとします。電車Cはどちらのコースを走るときも秒速25cmで進み、一定の速さで走るものとします。また、電車の長さは考えないものとします。
(1)
電車Aと電車Bだけが走る場合を考え、電車Aが駅を出発したあとに電車Bが駅を出発するものとします。また、ポイントは、外側のコースを走っていた電車は内側のコースに、内側のコースを走っていた電車は外側のコースに進むように切り替わるとします。次の問いに答えなさい。
①電車Aが駅を出発して再び駅に戻ってくるまでにかかる時間は何秒ですか。
②電車Aが駅を出発して2回目に地点Qに到達したときに、電車Bが1回目に地点Rに到達しました。電車Bは電車Aが出発して何秒後に駅を出発しましたか。
(2)
電車Aと電車Cだけが走る場合を考え、電車Aが駅を出発したあとに電車Cが駅を出発するものとします。また、ポイントは、直前にポイントを通過した電車の進んだコースと異なるコースに進むように切り替わり、最初にポイントを通過する電車は内側のコースに進むとします。次の問いに答えなさい。
①電車Aが1回目に駅を出発して連続して2回内側のコースを進むためには、電車Cは電車Aが出発して何秒後までに出発すればよいか、最大の整数の値を答えなさい。
②内側のコースの長さは10cmずつ変えることができるものとします。
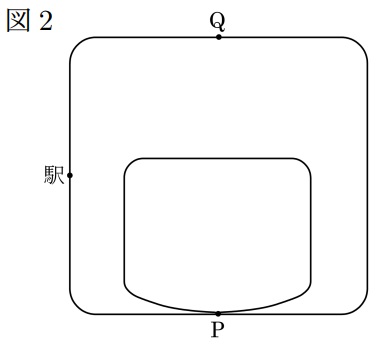
図2のように内側のコースの長さを〔 〕cm短くしました。最初に電車Aが駅を出発してから10秒後に電車Cが出発すると、電車Aは2回続けて内側のコースを進み、次は外側のコースを進みました。また、電車が地点Pを合計5回通過するまでに、電車A、Cの両方が外側のコース上にいる時間が連続して11秒以上になりました。〔 〕にあてはまる最小の整数の値を答えなさい。
@解説@
(1)
Aは外側と内側のコースすべてを周る。
外側の時間+内側の時間
=540÷30+400÷20
=18+20=38秒
②
AとBの速さは同じ。
AとBの距離の差を考える。

R―P間;400÷2=200cm
P―Q間;540÷2=270cm
駅で5秒間停車する点に注意!
270÷30+200÷20+5=24秒後
(2)①
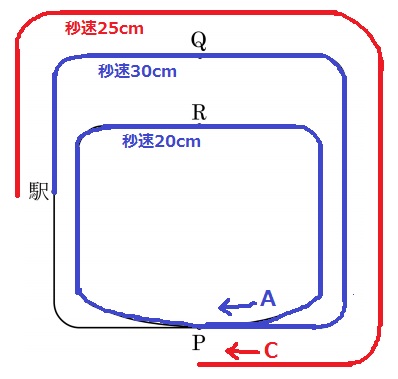
Aが2回目のPに触れる前に、CがPに触れる。
駅からPまでの外側の距離は、135+270=405m
Aが2回目のPに着くのは、405÷30+400÷20=33.5秒後
Cが1回目のPに着くのは、405÷25=16.2秒後
Aが出発してから、33.5-16.2=17.3秒後にCが出発すると、
ちょうどP地点でAとCが出会うことになる。
ということは、Cが先にPにつくにはそれよりも前の17秒後に出発すればいい。
②
かなり大変です:( ´ω` ):
本番では捨てて問題なし。
A、C両方が外側にいる時間が連続して11秒以上になるとき、
内側の長さを最小でいくら短くできるか。
駅~Pまでは405m。
Aは405÷30=13.5秒後にPに着いて内側へ移る。
CはAの10秒後に駅を出発するから、AC両方が外側にいるのは3.5秒間しかない。
⇒両方が外側に連続して11秒以上いるのはAが内側を2周した後。
ここで『電車が地点Pを合計5回通過した』に注目する。
最初にPに到着するのはA。
Aが2連続で内側をまわるには、Aより先にCがPに着く必要がある。(A→C)
内側を1周したAがPに着き、内側の2周目にはいる。(A→C→A)
内側を2周したAは次に外をまわる。(A→C→A→A)
では、5回目のPはAかCか。
Aはスタートから13.5秒後に1回目のPに着く。
CがはじめてPに着くのはAが出発してから、405÷25+10=16.2+10=26.2秒後
Aは26.2-13.5=12.7秒より長く内側を1周していないと、Cより先にPに着いてしまう。
ここで、AとCが内側を走らず、駅から外側のみを1周して、
さらにPに着くまでの時間(停車時間は含まない)を計算する。
距離は、540+405=945m
Aは945÷30=31.5秒
Cは945÷25=37.8秒
Cの方が6.3秒長くかかり、はじめの10秒遅れを含めると16.3秒差。
Aは12.7×2=25.4秒よりも長く内側を走っているから、
16.3<25.4よりAの方が遅れる→5回目にPに着くのはC。
【Pを通過する順;A⇒C⇒A⇒A⇒C】
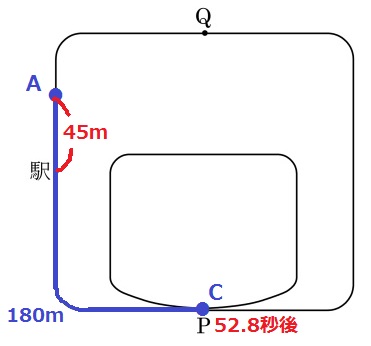
内側のコースを短くする長さは最小にする=内側のコースはできるだけ長くとる。
CがPに着いたとき、AとCが共に外側にいた時間がちょうど11秒となれば、
それほどAは内側を長い時間まわっていたことになる。
Aが内側から外側に移ったときから11秒後の位置は、
駅での停車時間を考慮すると、Pから30×(11-5)=180m先
駅から180-135=45m先の地点である。
Cが5回目のPに着く時刻は、Aが出発してから
(外側1周~P)+10秒遅れ+駅での停車
=37.8+10+5=52.8秒後
Aが移動する合計の時間は、駅での停車時間をのぞいて47.8秒間。
このうち、Aの外側の移動距離は、1周+45m=540+45=585m
Aの外側の移動時間は、585÷30=19.5秒間
Aの内側の移動時間は、47.8-19.5=28.3秒間
秒速20cmをかけると内側の長さ2周分になる。
内側1周の長さは、28.3×20÷2=283cm
内側のコースは10cm刻みで調節できる。
内側のコースを290cmにしてしまうと、Aが外側に出る時間が遅れてしまうので、
AとC両方が外側にいる時間が11秒より短くなってしまう。
⇒コースの内側の長さは280cm
内側のコースを短くする長さは、400-280=120cm



コメント