問題ＰＤＦ
下の【図１】のように、水平な机の上から４ｃｍの高さの位置に、
机と平行に張られたひもがあり、点Ａの位置に豆電球が取りつけられています。
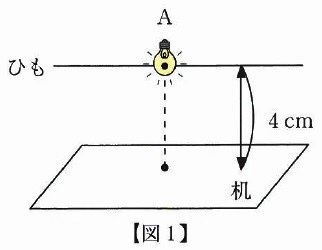
豆電球はひもにそって自由に動かすことができます。机の上にある立体を置き、豆電球に明かりをつけたときに机の上にできる立体の影について考えます。ただし、影はすべて机に写るものとし、机に接している立体の底面部分は影とみなしません。
はじめに、上の【図２】のように、一辺の長さが３ｃｍの立方体を机の上に置きました。この立方体は、真上から見たとき、立方体の上面の辺ＰＱの真ん中の点が、点Ａのちょうど真下で、辺ＰＱがひもに垂直になるように置いてあります。
その後、豆電球を点Ａの位置から点Ｂの位置に移動してから明かりをつけました。
真上から見ると、机の上には、下の【図３】の斜線部分のような影の図形ができました。
（１）
【図３】の影のＲＳの長さは〔 〕ｃｍです。
また、【図２】のひもの点Ａから点Ｂまでの長さは〔 〕ｃｍです。
豆電球を点Ａの位置に戻します。
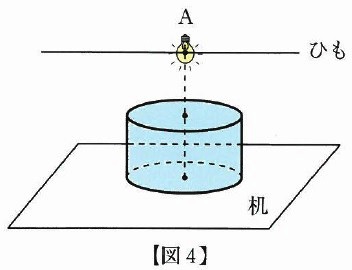
次は、上の【図４】のように、半径が２ｃｍ、高さが２ｃｍの円柱を、
底面の円の中心が点Ａの真下にくるように置きました。
（２）
点Ａの位置で豆電球に明かりをつけたとき、
机の上に円柱の影でできる図形の面積は〔 〕ｃｍ2です。
（３）
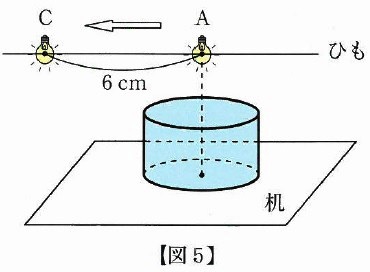
上の【図５】のように、点Ａの位置で豆電球の明かりをつけたまま、
６ｃｍ離れた点Ｃの位置までひもにそって豆電球を移動すると、
机の上にできる円柱の影も移動します。
このとき、机の上にできる影が通過したすべての部分の面積は〔 〕ｃｍ2です。
＠解説＠
（１）
はじめは横から見る。
高さが１ｃｍと３ｃｍ→辺の比が１：３である直角三角形の相似。
今度は上から。
△ＢＰＱと△ＢＴＵの相似で、ＰＱ：ＴＵ＝ＢＰ：ＢＴ＝①：④
ＴＵ＝３×④/①＝12ｃｍ
ＲＳ＝ＴＵ＝12ｃｍ
真上からみる。光源Ｂから正方形を投影したものが四角形ＳＲＴＵ。
→四角形ＳＲＴＵは正方形。
ＴＲ＝12ｃｍ
【３】＝48－12＝36ｃｍ
ＡＢ＝【１】＝12ｃｍ
（２）
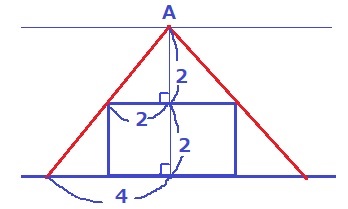
横からみる。
辺の比が１：２の直角三角形を見つけ、底辺の半径は４ｃｍ。
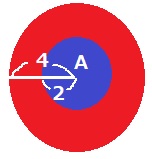
上からみると、赤い部分が影ができるところ。
半径４ｃｍの円から半径２ｃｍの円をひく。
４×４×3.14－２×２×3.14
＝12×3.14＝37.68ｃｍ2
（３）
斜めから円柱に光をあてたとき、影はどういう形になるか。
やや初見殺しなので、初めてのひとはこれを機におさえておきたい(´ﾟдﾟ｀)
光源が円柱の上にある場合。
Ａの左側Ａ’、Ａ’’に光源を移動させたとする。
光源の高さは6ｃｍ、円柱の高さは３ｃｍだから、横からみたときの辺の比は常に１：２。
上からみると、光源Ａ’、Ａ’’から円周上にある任意の点までの距離は、
円周上の任意の点から影の先端までの距離とすべて１：１で等しくなる！
つまり、影は大きな円となり、その半径は円柱の２倍。
光源が円柱の外側の上にある場合。
円柱に接する接線を作図する。円柱の影は太線で囲まれたエリア。
接線と半径は直交し、辺の比が１：２の直角三角形の相似が見つかる。
光源を左に移動させるほど、より斜めから円柱に光をあてるので影は右に伸びるが、
右端の円の半径は常に４ｃｍである。
本問の影の軌跡をとらえる。
ゴール時も半径４ｃｍなので、ドーナッツ型の状態から半径４ｃｍの円が右に平行移動する。
影の円の中心の移動距離は６ｃｍで、移動後の影の円は円柱の右側で接することになる。
斜線が求積すべきエリア。
留意点は円柱のあるところは影ができない！
問題文→『影はすべて机に写るものとし、机に接している立体の底面部分は影とみなしません』
この図形は（２）のドーナッツに６×８の長方形を加えたものとなる。
したがって、37.68＋６×８＝85.68ｃｍ2
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント