問題ＰＤＦ
（１）
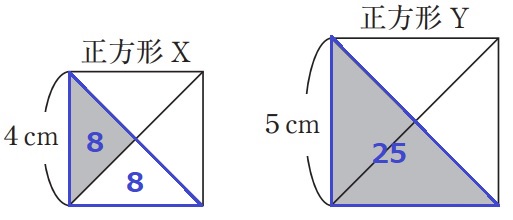
図１のように、一辺の長さが４ｃｍの正方形Ｘと、一辺の長さが５ｃｍの正方形Ｙがあり、
それぞれに２本の対角線を引いてあります。
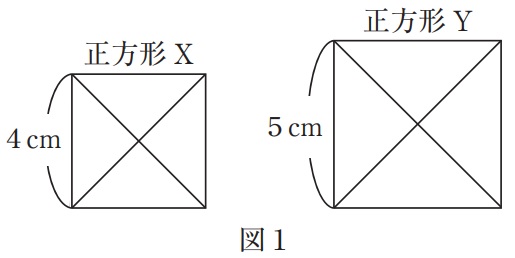
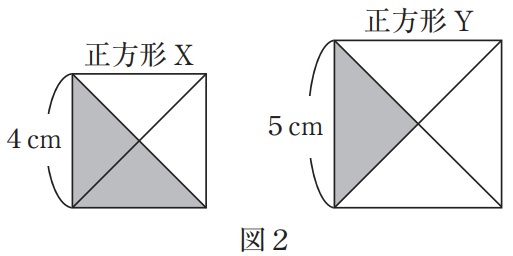
①図２において、正方形Ｘの影の部分と正方形Ｙの影の部分の面積の比を、
もっとも簡単な整数の比で答えなさい。
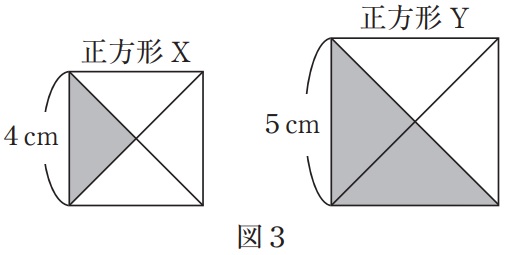
②図３において、正方形Ｘの影の部分と正方形Ｙの影の部分の面積の比を、
もっとも簡単な整数の比で答えなさい。
（２）
図４のように、２つの直角二等辺三角形ＡＢＣ、ＤＥＦがあります。
三角形ＡＢＣと三角形ＤＥＦの面積の比は18：25です。
①ＡＢ：ＤＦの長さの比を、もっとも簡単な整数の比で答えなさい。
②ＡＣとＤＥの長さの比を、もっとも簡単な整数の比で答えなさい。
（３）
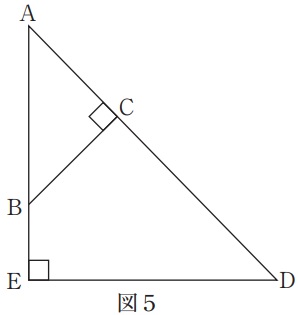
図５のように、２つの直角二等辺三角形ＡＢＣ、ＡＤＥがあります。
三角形ＡＢＣと三角形ＡＤＥの面積の比は25：98です。
ＡＢとＡＥの長さの比を、もっとも簡単な整数の比で答えなさい。
（４）
図６のように、２つの直角三角形ＡＢＣ、ＡＤＥがあります。
三角形ＢＥＦと三角形ＤＦＣの面積の比は49：50です。
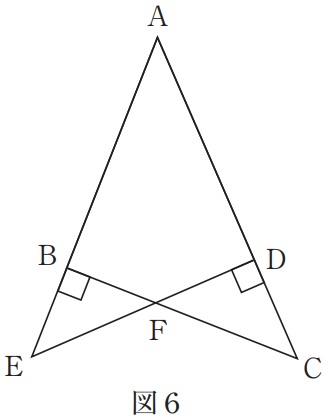
①ＡＢとＢＥの長さの比を、もっとも簡単な整数の比で答えなさい。
②三角形ＡＢＣと三角形ＡＤＥの面積の比を、もっとも簡単な整数の比で答えなさい。
＠解説＠
（１）①
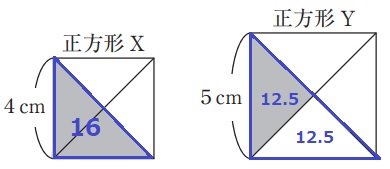
青線の直角二等辺三角形の面積比は16：25。
25÷２＝12.5だから、
16：12.5
＝32：25
②
同様の考えで８：25。
（２）①
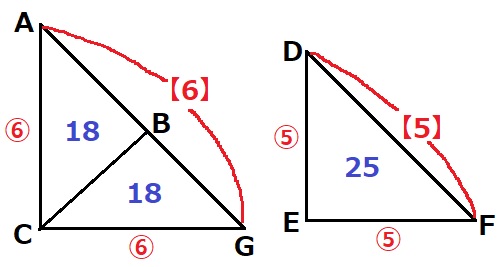
面積比が平方数であると嬉しい。
そこで、前問のように直角二等辺ＡＢＣを２個くっつけて直角二等辺ＡＣＧにする。
すると、△ＡＣＧと△ＤＥＦの面積比が36：25⇒辺の比は⑥：⑤
ＡＧ：ＤＦ＝【６】：【５】
ＢはＡＧの中点なので、ＡＢ：ＤＦ＝３：５
②
前問の図で既出。
ＡＣ：ＤＥ＝６：５
（３）
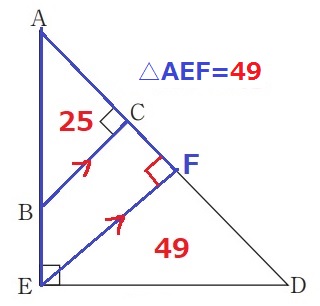
98÷２＝49 ←平方数に着目
直角二等辺ＡＤＥを半分に割って、直角二等辺ＡＥＦをつくる。
△ＡＢＣと△ＡＥＦは相似で面積比は25：49。
辺の比であるＡＢ：ＡＥ＝５：７
（４）①
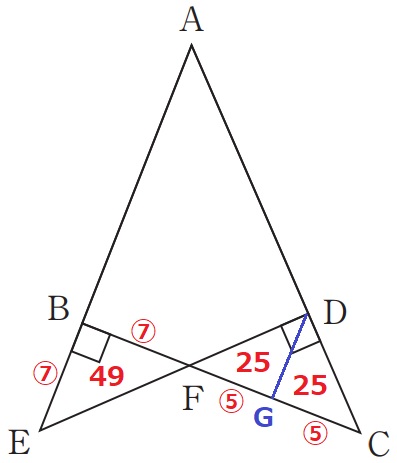
50÷２＝25 ←平方数！
直角二等辺ＣＤＦを真っ二つにして、直角二等辺ＤＣＧ・ＤＦＧをつくる。
直角二等辺の等辺の比ＢＦ：ＦＧ（ＧＣ）＝⑦：⑤
ＡＢ＝ＣＢ＝⑰
ＡＢ：ＢＥ＝17：７
②
等辺〇×等辺〇＝直角二等辺の面積比だから、
△ＡＢＣの面積比は⑰×⑰＝289
△ＡＢＣと△ＡＤＥは四角形ＡＢＦＤを共通とし、違いは△ＢＥＦと△ＤＦＣ。
差が－１なので、△ＡＤＥの面積比は289－１＝288
△ＡＢＣ：△ＡＤＥ＝289：288
難関中（算数科）解説ページに戻る
コメント