問題ＰＤＦ
直方体の形をした、２つの容器Ａ、Ｂに水が入っています。この２つの容器の底面積は異なり、容器Ａの底面積は120ｃｍ2です。
はじめ、２つの容器ＡとＢの水の深さの比は３：２でした。Ａに入っている水の量の１/６をＢへ移したところ、Ａの水の深さはＢより0.8ｃｍだけ深くなりました。さらに、Ａに入っている水の量の１/５をＢへ移すと、Ｂの水の深さはＡより2.4ｃｍ深くなりました。
（１）
はじめに容器Ａ、Ｂに入っていた水の深さをそれぞれ答えなさい。
（２）
２つの容器の水の深さを等しくするには、この後、ＢからＡへ何ｃｍ3の水を移せばよいですか。
（１）
ＡとＢの水の量は等しいとは限らない。
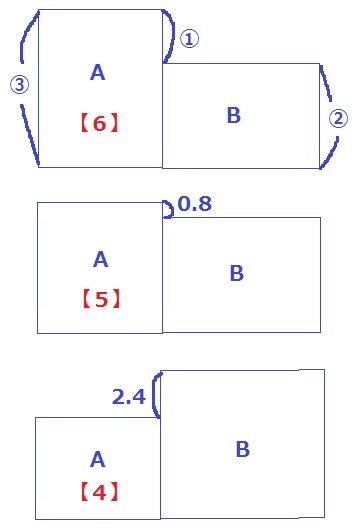
はじめのＡの量を【６】とする。
【１】をＢに移してＡの量が【５】になったとき、Ａ＞Ｂで差は0.8ｃｍ。
【５】の１/５をＢに移動。移動する水の量は【１】で先ほどと同じ量。
Ａの量が【４】になったとき、Ａ＜Ｂで差は2.4ｃｍ。
Ａが【５】→【４】に変化したとき、Ｂを基準にＡは＋0.8から－2.4に下がる。
ということは、【１】の移動でＡとＢの差は2.4＋0.8＝3.2ｃｍずつ拡大する。
【５】のときから逆再生してＡを【６】に戻すと、ＡとＢの差は0.8＋3.2＝４ｃｍ
これが初期状態におけるＡとＢの差の①に相当する。
③＝４×３＝12ｃｍ、②＝４×２＝８ｃｍ
Ａ…12ｃｍ、Ｂ…８ｃｍ
（２）
Ａが【５】のとき、Ａ＞Ｂで差が0.8ｃｍであった。
もし、この状態からＡとＢの水深を等しくするには、
Ａからどれほどの量をＢに移動させるべきであったか？
【１】で差が3.2ｃｍ拡大するから、0.8ｃｍでは【0.8/3.2】＝【１/４】
ということは、余分に移してしまった【３/４】をＢから戻せばいい。
はじめのＡの水の量が【６】なので、
120×12×１/６×３/４＝180ｃｍ3
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント